
【题目】某兴趣小组欲研究某地区昼夜温差大小与患感冒就诊人数之间的关系,他们分别到气象局与某医院抄录了1到5月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 |
昼夜温差 | 8 | 10 | 13 | 12 | 9 |
就诊人数 | 18 | 25 | 28 | 26 | 17 |
该兴趣小组确定的研究方案是:先从这5组数据中选取一组,用剩下的4组数据求线性回归方程,再用选取的一组数据进行检验.
(1)若选取的是1月的一组数据,请根据2至5月份的数据.求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2,则认为得到的线性回归方程是理想的,试判断该小组所得的线性回归方程是否理想?如果不理想,请说明理由,如果理想,试预测昼夜温差为![]() 时,因感冒而就诊的人数约为多少?
时,因感冒而就诊的人数约为多少?
参考公式: ,
, ![]() .
.
科目:高中数学 来源: 题型:
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用下图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表:
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”?并写出简要分析.
附参考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的单调函数,且对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=3,则方程f(x)﹣f′(x)=2的解所在的区间是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(1,2)
D.(2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() ,且直线
,且直线![]() 有唯一的一个点
有唯一的一个点![]() ,使得过
,使得过![]() 点作圆
点作圆![]() 的两条切线互相垂直,则
的两条切线互相垂直,则![]() _____;设
_____;设![]() 是直线
是直线![]() 上的一条线段,若对于圆
上的一条线段,若对于圆![]() 上的任意一点
上的任意一点![]() ,则
,则![]() 的最小值_____.
的最小值_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )ax , a为常数,且函数的图象过点(﹣1,2).
)ax , a为常数,且函数的图象过点(﹣1,2).
(1)求a的值;
(2)若g(x)=4﹣x﹣2,且g(x)=f(x),求满足条件的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(Ⅰ)证明:平面ACD⊥平面ABC;
(Ⅱ)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D﹣AE﹣C的余弦值.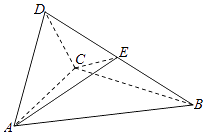
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥PB,PC=2. 
(1)求证:平面PAB⊥平面ABCD;
(2)若PA=PB,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com