
(05年福建卷理)(14分)
已知数列{an}满足a1=a, an+1=1+![]() 我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:
我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:![]()
(Ⅰ)求当a为何值时a4=0;
(Ⅱ)设数列{bn}满足b1=-1, bn+1=![]() ,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
(Ⅲ)若![]() ,求a的取值范围.
,求a的取值范围.
解析:(Ⅰ)∵a1=a,∴1+![]() =a2,∴a2=
=a2,∴a2=![]() ,
,![]() ,
,![]() ,
,
故当![]() 时,
时,![]()
(Ⅱ)∵b1=-1,![]()
当a=b1时,a1=1+![]() =0
=0
当a=b2时,a2=![]() =b1,∴a2=0,
=b1,∴a2=0,
当a=b3时,a3=1+![]() =b2,∴a3=1+
=b2,∴a3=1+![]() ,∴a4=0,
,∴a4=0,
……
一般地,当a=bn时,an+1=0,可得一个含育n+1项的有穷数列a1,a2,a3,…,an+1.
可用数学归纳法加以证明:
① 当n=1时,a=b1,显然a2=0,得到一个含2项的有穷数列a1,a2.
② 假设当n=k时,a=bk,得到一个含有k+1项的有穷数列a1,a2,a3,…,ak+1,其中ak+1=0,则n=k+1时.a=bk+1,∴a2=1+![]() .
.
由假设可知,可得到一个含有k+1项的有穷数列a2,a3,…,ak+2,其中ak+2=0.
由①②知,对一切n∈N+,命题都成立.
(Ⅲ)要使![]() 即
即![]() ,∴1<an-1<2.
,∴1<an-1<2.
∴要使![]() ,当且仅当它的前一项an-1,满足1<an-1<2,∵(
,当且仅当它的前一项an-1,满足1<an-1<2,∵(![]() ,2)
,2)![]() (1,2),
(1,2),
∴只须当a4![]() ,都有
,都有![]()
由![]() 得
得![]() ,
,
解不等式组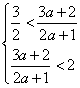 得
得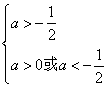 ,故a>0.
,故a>0.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
(09年江苏百校样本分析)(10分)挑选空军飞行学员可以说是“万里挑一”,要想通过需过“五关”――目测、初检、复检、文考、政审等. 某校甲、乙、丙三个同学都顺利通过了前两关,有望成为光荣的空军飞行学员. 根据分析,甲、乙、丙三个同学能通过复检关的概率分别是0.5,0.6,0.75,能通过文考关的概率分别是0.6,0.5,0.4,通过政审关的概率均为1.后三关相互独立.
(1)求甲、乙、丙三个同学中恰有一人通过复检的概率;
(2)设通过最后三关后,能被录取的人数为![]() ,求随机变量
,求随机变量![]() 的期望
的期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年莆田四中一模理) (14分)
由函数![]() 确定数列
确定数列![]() ,
,![]() ,若函数
,若函数![]() 的反函数
的反函数![]() 能确定数列
能确定数列![]() ,
,![]() ,则称数列
,则称数列![]() 是数列
是数列![]() 的“反数列”。
的“反数列”。
(1)若函数![]() 确定数列
确定数列![]() 的反数列为
的反数列为![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)对(1)中![]() ,不等式
,不等式![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的范围;
的范围;
(3)设![]() ,若数列
,若数列![]() 的反数列为
的反数列为![]() ,
,![]() 与
与![]() 的公共项组成的数列为
的公共项组成的数列为![]() ;求数列
;求数列![]() 前
前![]() 项和
项和![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com