
 =(
=( sin2x,-f(x)),
sin2x,-f(x)), =(-m,cos2x+m-
=(-m,cos2x+m- )(m∈R) 且
)(m∈R) 且 与
与 互为相反向量.
互为相反向量. ),f2(x)-λf(x)+1的最小值为-2,求实数λ的值.
),f2(x)-λf(x)+1的最小值为-2,求实数λ的值. 与
与 互为相反向量可得 m=
互为相反向量可得 m= sin2x,f(x)=cos2x+m-
sin2x,f(x)=cos2x+m- ,
,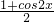 +
+ sin2x-
sin2x- =sin(2x+
=sin(2x+ ).
). ),∴2x+
),∴2x+ ∈[
∈[ ,
, ),∴
),∴ ≤sin(2x+
≤sin(2x+ )≤1,即f(x)∈[
)≤1,即f(x)∈[ ,1].
,1]. <
< 时,则h在[
时,则h在[ ,1]上是增函数,则f(x)=
,1]上是增函数,则f(x)= 时,h取得最小值为-2,
时,h取得最小值为-2, -
- λ+1=-2,解得 λ=
λ+1=-2,解得 λ= (舍去).
(舍去). ≤
≤ ≤1时,f(x)=
≤1时,f(x)= 时,h取得最小值为-2,即
时,h取得最小值为-2,即 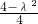 =-2,解得λ=±2
=-2,解得λ=±2 (舍去).
(舍去). >1时,h在[
>1时,h在[ ,1]上是减函数,f(x)=1 时,h取得最小值为 1-λ+1=-2,解得 λ=4.
,1]上是减函数,f(x)=1 时,h取得最小值为 1-λ+1=-2,解得 λ=4. 与
与 互为相反向量可得 m=
互为相反向量可得 m= sin2x,f(x)=cos2x+m-
sin2x,f(x)=cos2x+m- ,化简可得f(x)的解析式.
,化简可得f(x)的解析式. ),可得f(x)∈[
),可得f(x)∈[ ,1],令 h=f2(x)-λf(x)+1,利用二次函数的性质求得h的最小值,再由最小值为-2求得实数λ的值.
,1],令 h=f2(x)-λf(x)+1,利用二次函数的性质求得h的最小值,再由最小值为-2求得实数λ的值.

科目:高中数学 来源: 题型:
| a |
| π |
| 6 |
| π |
| 6 |
| b |
| π |
| 6 |
| π |
| 6 |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| π |
| 8 |
| π |
| 8 |
| b |
| π |
| 8 |
| a |
| b |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| π |
| 2 |
| a |
| b |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:辽宁省大连市、沈阳市2012届高三第二次联合考试数学文科试题 题型:044
已知向量m=(sin2+![]() ,sinx),n=(
,sinx),n=(![]() cos2x-
cos2x-![]() sin2x,2sinx),函数f(x)=m·n.
sin2x,2sinx),函数f(x)=m·n.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若![]() ,求函数f(x)值域.
,求函数f(x)值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com