
已知等差数列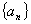 满足:
满足: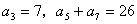 ,
,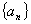 的前
的前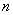 项和为
项和为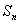 。
。
(1)求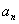 及
及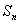 ;
;
(2)令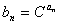 (其中
(其中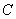 为常数,且
为常数,且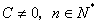 ),求证数列
),求证数列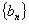 为等比数列。
为等比数列。
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
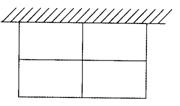
如图所示,动物园要围成四间相同面积的长方形虎笼,一面可利用原有的墙,其它各面用钢筋网围成。现有36m长的钢筋网材料,则可围成的每间虎笼面积最大为_________m2。
查看答案和解析>>
科目:高中数学 来源: 题型:
设向量a=(cos2x,37,sin2x),b=(cos2x,-sin2x),函数f(x)=a·b,则函数f(x)的图象( )
A. 关于点(π,0)中心对称 B. 关于点(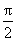 ,0)中心对称
,0)中心对称
C. 关于点(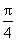 ,0)中心对称 D. 关于点(0,0)中心对称
,0)中心对称 D. 关于点(0,0)中心对称
查看答案和解析>>
科目:高中数学 来源: 题型:
一般地,我们把函数h(x)=anxn+an-1xn-1+…+a1x+a0 (n∈N)称为多项式函数,其中系数a0,a1,…,an∈R。
设f(x),g(x)为两个多项式函数,且对所有的实数x等式f[g(x)]=g[f(x)]恒成立。
(I)若f(x)=x2+3,g(x)=kx+b(k≠0)。
①求g(x)的表达式;
②解不等式f(x)-g(x)>5。
(II)若方程f(x)=g(x)无实数解,证明方程f[f(x)]=g[g(x)]也无实数解。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com