已知平面内两向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，且0＜α＜β＜π．
(1)证明：(a＋b)⊥(a－b)；
(2)若两个向量ka＋b与a－kb的模相等(k≠0)，求证：a⊥b．
|
证明：(1)a＝(cosα，sinα)，b＝(cosβ，sinβ)， ∴a＋b＝(cosα＋cosβ，sinα＋sinβ)， a－b＝(cosα－cosβ，sinα－sinβ)． ∴(a＋b)·(a－b)＝cos2α－cos2β＋sin2α－sin2β＝1－1＝0． ∴(a＋b)⊥(a－b)． (2)∵(ka＋b)2＝|ka＋b|2＝k2a2＋2ka·b＋b2， |a－kb|2＝a2－2ka·b＋k2b2， 又|ka＋b|＝|a－kb|， ∴k2a2＋2ka·b＋b2＝a2－2ka·b＋k2b2， (k2－1)a2＋4ka·b＋(1－k2)b2＝0． 又|a|＝|b|＝1， ∴4ka·b＝0． ∵k≠0， ∴a·b＝0， ∴a⊥b． |
发散思维新课堂系列答案科目：高中数学 来源：山东省枣庄市2010届高三第一次模拟考试数学理科试题 题型：013
已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a＋
)·(b＋
)＝0，则|c|的最大值是
2
4
查看答案和解析>>
科目：高中数学 来源：2010-2011年福建省南安一中高一下学期期末考试数学 题型：单选题
已知平面直角坐标系内的两个向量
＝（1，2），
＝（m，3m－2），且平面内的任一向量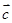
都可以唯一的表示成＝λ＋μ（λ，μ为实数），则m的取值范围是（ ）
| A．（－∞，2） | B．（2，＋∞） |
| C．（－∞，＋∞） | D．（－∞，2）∪（2，＋∞） |
查看答案和解析>>
科目：高中数学 来源：2012年人教A版高中数学必修四2.4平面向量的数量积练习卷（二）（解析版） 题型：选择题
(08·浙江)已知a、b是平面内两个互相垂直的单位向量，若向量c满足(a－c)·(b－c)＝0，则|c|的最大值是( )
A．1 B．2
C. 
D. 
查看答案和解析>>
科目：高中数学 来源：2010-2011年福建省高一下学期期末考试数学 题型：选择题
已知平面直角坐标系内的两个向量
＝（1，2），
＝（m，3m－2），且平面内的任一向量
都可以唯一的表示成＝λ＋μ（λ，μ为实数），则m的取值范围是（ ）zxxk
A．（－∞，2） B．（2，＋∞）
C．（－∞，＋∞） D．（－∞，2）∪（2，＋∞）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com