
平面内有n(n∈N+,n≥2)条直线,其中任何两条不平行,任何三条不过
同一点,证明:交点的个数f(n)= .
.
见解析
【解析】(1)当n=2时,两条直线的交点只有一个,
又f(2)=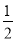 ×2×(2-1)=1,
×2×(2-1)=1,
∴当n=2时,命题成立.
(2)假设n=k,∈N+,且(k>2)时,命题成立,即平面内满足题设的任何k条直线交点个数f(k)=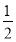 k(k-1),
k(k-1),
那么,当n=k+1时,任取一条直线l,除l以外其他k条直线交点个数为f(k)=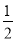 k(k-1),l与其他k条直线交点个数为k,从而k+1条直线共有f(k)+k个交点,
k(k-1),l与其他k条直线交点个数为k,从而k+1条直线共有f(k)+k个交点,
即f(k+1)=f(k)+k=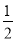 k(k-1)+k=
k(k-1)+k=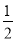 k(k-1+2)=
k(k-1+2)=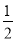 k(k+1)=
k(k+1)=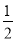 (k+1)[(k+1)-1],
(k+1)[(k+1)-1],
这表明,当n=k+1时,命题成立.
由(1)、(2)可知,对n∈N+(n≥2)命题都成立.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:2015届辽宁省沈阳市高二质量监测文科数学试卷(解析版) 题型:选择题
若一个动点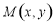 到两个定点
到两个定点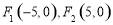 的距离之差的绝对值等于8,则动点M的轨迹方程为 ( )
的距离之差的绝对值等于8,则动点M的轨迹方程为 ( )
A.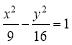 B.
B.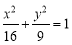
C.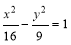 D.
D.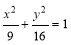
查看答案和解析>>
科目:高中数学 来源:2015届辽宁大连普通高中高二上学期期末考试文数学卷(解析版) 题型:选择题
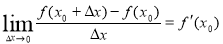 ,其中
,其中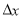 ( )
( )
(A)恒取正值或恒取负值 (B)有时可以取0
(C)恒取正值 (D)可以取正值和负值,但不能取0
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6章末练习卷(解析版) 题型:选择题
某个命题与正整数有关,如果当n=k(k∈N+)时,该命题成立,那么可
推得当n=k+1时命题也成立.现在已知当n=5时,该命题不成立,那么可推得( ).
A.当n=6时该命题不成立
B.当n=6时该命题成立
C.当n=4时该命题不成立
D.当n=4时该命题成立
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6.3练习卷(解析版) 题型:解答题
已知,n∈N+,An=2n2,Bn=3n,试比较An与Bn的大小,
并加以证明.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6.2练习卷(解析版) 题型:填空题
已知函数f(x)在[0,1]上有意义,且f(0)=f(1),如果对任意的x1,x2∈[0,1]
且x1≠x2,都有|f(x1)-f(x2)|<|x1-x2|,求证:|f(x1)-f(x2)|<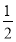 ,若用反证法证明该题,则反设应为________.
,若用反证法证明该题,则反设应为________.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6.1练习卷(解析版) 题型:解答题
在数列{an}中,a1=1,an+1=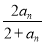 ,n∈N+,求a2,a3,a4
,n∈N+,求a2,a3,a4
并猜想数列的通项公式,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com