
【题目】已知函数![]()
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)见解析(2)![]()
【解析】
试题分析:(1)先求函数导数![]() ,再按导函数零点讨论:若
,再按导函数零点讨论:若![]() ,无零点,单调;若
,无零点,单调;若![]() ,一个零点
,一个零点![]() ,先减后增;若
,先减后增;若![]() ,一个零点
,一个零点![]() ,先减后增;(2)由单调性确定函数最小值:若
,先减后增;(2)由单调性确定函数最小值:若![]() ,满足;若
,满足;若![]() ,最小值为
,最小值为![]() ,即
,即![]() ;若
;若![]() ,最小值为
,最小值为![]() ,即
,即![]() ,综合可得
,综合可得![]() 的取值范围为
的取值范围为![]() .
.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
①若![]() ,则
,则![]() ,在
,在![]() 单调递增.
单调递增.
②若![]() ,则由
,则由![]() 得
得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
③若![]() ,则由
,则由![]() 得
得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)①若![]() ,则
,则![]() ,所以
,所以![]() .
.
②若![]() ,则由(1)得,当
,则由(1)得,当![]() 时,
时,![]() 取得最小值,最小值为
取得最小值,最小值为![]() .从而当且仅当
.从而当且仅当![]() ,即
,即![]() 时,
时,![]() .
.
③若![]() ,则由(1)得,当
,则由(1)得,当![]() 时,
时,![]() 取得最小值,最小值为
取得最小值,最小值为![]() .从而当且仅当
.从而当且仅当![]() ,即
,即![]() 时
时![]() .
.
综上,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】(10分)四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.

(1)求四面体ABCD的体积;
(2)证明:四边形EFGH是矩形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《最强大脑》是江苏卫视引进德国节目《SuperBrain》而推出的大型科学竞技真人秀节目.节目筹备组透露挑选选手的方式:不但要对空间感知、照相式记忆进行考核,而且要让选手经过名校最权威的脑力测试,120分以上才有机会入围.某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各100名,然后对这200名学生进行脑力测试.规定:分数不小于120分为“入围学生”,分数小于120分为“未入围学生”.已知男生入围24人,女生未入围80人.
(1)根据题意,填写下面的![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 以上的把握认为脑力测试后是否为“入围学生”与性别有关;
以上的把握认为脑力测试后是否为“入围学生”与性别有关;
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | 24 | ||
女生 | 80 | ||
总计 |
(2)用分层抽样的方法从“入围学生”中随机抽取11名学生,然后再从这11名学生中抽取3名参加某期《最强大脑》,设抽到的3名学生中女生的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: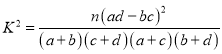 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在某条商业街分别开有两家业务上有关联的零售商店,这两家商店的日纯利润变化情况如下表所示:

(1)从这几天的日纯利润来看,哪一家商店的日平均纯利润多些?
(2)由表中数据可以认为这两家商店的日纯利润之间有较强的线性相关关系.
(ⅰ)试求![]() 与
与![]() 之间的线性回归方程;
之间的线性回归方程;
(ⅱ)预测当![]() 店日纯利润不低于2万元时,
店日纯利润不低于2万元时,![]() 店日纯利润的大致范围(精确到小数点后两位);
店日纯利润的大致范围(精确到小数点后两位);
(3)根据上述5日内的日纯利润变化情况来看,哪家商店经营状况更好?
附:线性回归方程![]() 中,
中,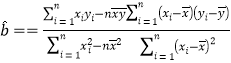 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
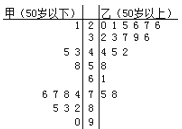
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com