
某中学从高中三个年级选派4名教师和20名学生去当文明交通宣传志愿者,20名学生的名额分配为高一12人,高二6人,高三2人.
(1)若从20名学生中选出3人做为组长,求他们中恰好有1人是高一年级学生的概率;
(2)若将4名教师随机安排到三个年级(假设每名教师加入各年级是等可能的,且各位教师的选择是相互独立的),记安排到高一年级的教师人数为X,求随机变量X的分布列和数学期望.
(1) 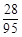 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)从高一12人中选出1人,从高二和高三共8人中选出2人的事件为A,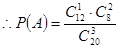 ,计算得到结果;(2)每位教师选择高一年级的概率均为
,计算得到结果;(2)每位教师选择高一年级的概率均为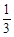 ,并且相互独立,X的所有取值为0,1,2,3,4.
,并且相互独立,X的所有取值为0,1,2,3,4.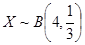 ,
, ,
,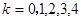 ,然后列出随机变量X的概率分布列,利用
,然后列出随机变量X的概率分布列,利用 ,或是利用二项分布的期望公式
,或是利用二项分布的期望公式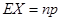 ,得出结果.随机变量的概率,分布列,期望还是高考的重点内容,属于基础题型,
,得出结果.随机变量的概率,分布列,期望还是高考的重点内容,属于基础题型,
试题解析:(1)解:设 “他们中恰好有1人是高一年级学生” 为事件 ,
,
则  .
.
所以恰好有1人是高一年级学生的概率为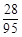 . 4分
. 4分
(2)解:X的所有取值为0,1,2,3,4. 6分
由题意可知,每位教师选择高一年级的概率均为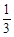 , 7分
, 7分
所以 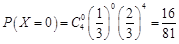 ;
;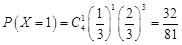
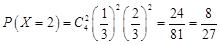 ;
;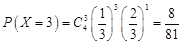 ;
;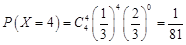 .
.
随机变量X的分布列为:
12分X 0 1 2 3 4 P 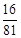
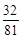
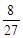
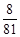
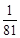
所以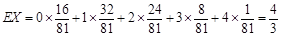 . 13分
. 13分
考点:1.超几何分布;2.二项分布.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:解答题
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下:
甲运动员
| 射击环数 | 频数 | 频率 |
| 7 | 10 | 0.1 |
| 8 | 10 | 0.1 |
| 9 | x | 0.45 |
| 10 | 35 | y |
| 合计 | 100 | 1 |
| 射击环数 | 频数 | 频率 |
| 7 | 8 | 0.1 |
| 8 | 12 | 0.15 |
| 9 | z | |
| 10 | | 0.35 |
| 合计 | 80 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
每年的3月12日,是中国的植树节.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗的高度,规定高于128厘米的树苗为“良种树苗”,测得高度如下(单位:厘米):
甲:137,121,131,120,129,119,132,123,125,133;
乙:110,130,147,127,146,114,126,110,144,146.
(1)根据抽测结果,画出甲、乙两种树苗高度的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出对两种树苗高度的统计结论;
(2)设抽测的10株甲种树苗高度平均值为 ,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
(3)若小王在甲种树苗中随机领取了5株进行种植,用样本的频率分布估计总体分布,求小王领取到的“良种树苗”的株数X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,ξ=0;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,ξ=1.
(1)求概率P(ξ=0);
(2)求ξ的分布列,并求其数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
假设某班级教室共有4扇窗户,在每天上午第三节课上课预备铃声响起时,每扇窗户或被敞开或被关闭,且概率均为0.5.记此时教室里敞开的窗户个数为X.
(1)求X的分布列;
(2)若此时教室里有两扇或两扇以上的窗户被关闭,班长就会将关闭的窗户全部敞开,否则维持原状不变.记每天上午第三节课上课时该教室里敞开的窗户个数为Y,求Y的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
| 指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 8 | 20 | 42 | 22 | 8 |
| 指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 4 | 12 | 42 | 32 | 10 |
 从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
市民李先生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机的.同一条道路去程与回程是否堵车相互独立.假设李先生早上需要先开车送小孩去丙地小学,再返回经甲地赶去乙地上班.假设道路A,B,D上下班时间往返出现拥堵的概率都是 ,道路C,E上下班时间往返出现拥堵的概率都是
,道路C,E上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
(1)求李先生的小孩按时到校的概率;
(2)李先生是否有七成把握能够按时上班?
(3)设X表示李先生下班时从单位乙到达小学丙遇到拥堵的次数,求X的均值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为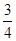 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为 ,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(1)求该射手恰好命中两次的概率;
(2)求该射手的总得分X的分布列及数学期望E(X);
(3)求该射手向甲靶射击比向乙靶射击多击中一次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
湖南省在学业水平考查中设计了物理学科的实验考查方案:考生从 道备选试验考查题中一次随机抽取
道备选试验考查题中一次随机抽取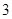 题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中
题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中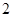 题便通过考查.已知
题便通过考查.已知 道备选题中文科考生甲有
道备选题中文科考生甲有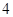 题能正确完成,
题能正确完成,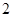 题不能完成;文科考生乙每题正确完成的概率都是
题不能完成;文科考生乙每题正确完成的概率都是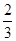 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(Ⅰ)分别写出文科考生甲正确完成题数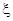 和文科考生乙正确完成题数
和文科考生乙正确完成题数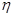 的概率分布列,并计算各自的数学期望;
的概率分布列,并计算各自的数学期望;
(Ⅱ)试从两位文科考生正确完成题数的数学期望及通过考查的概率分析比较这两位考生的实验操作能力.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com