练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    现有甲、乙两个靶．某射手向甲靶射击两次，每次命中的概率为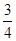，每命中一次得1分，没有命中得0分；向乙靶射击一次，命中的概率为，命中得2分，没有命中得0分，该射手每次射击的结果相互独立．假设该射手完成以上三次射击．
    (1)求该射手恰好命中两次的概率；
    (2)求该射手的总得分X的分布列及数学期望E(X)；
    (3)求该射手向甲靶射击比向乙靶射击多击中一次的概率．

    （1）（2）（3）

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某中学从高中三个年级选派4名教师和20名学生去当文明交通宣传志愿者，20名学生的名额分配为高一12人，高二6人，高三2人．
    （1）若从20名学生中选出3人做为组长，求他们中恰好有1人是高一年级学生的概率；
    （2）若将4名教师随机安排到三个年级（假设每名教师加入各年级是等可能的，且各位教师的选择是相互独立的），记安排到高一年级的教师人数为X，求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    辽宁某大学对参加全运会的志愿者实施“社会教育实践”学分考核，因该批志愿者表现良好，该大学决定考核只有合格和优秀两个等次，若某志愿者考核为合格，授予0.5个学分；考核为优秀，授予1个学分，假设该校志愿者甲、乙、丙考核为优秀的概率分别为、、，他们考核所得的等次相互独立．
    (1)求在这次考核中，志愿者甲、乙、丙三人中至少有一名考核为优秀的概率；
    (2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量X，求随机变量X的分布列．
    (3)求X的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某班同学利用寒假进行社会实践，对年龄在的人群随机抽取人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
       
    （1）补全频率分布直方图，并求的值；
    （2）从年龄在的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动，其中选取2人作为领队，求选取的2名领队中恰有1人年龄在的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    盒子中装有四张大小形状均相同的卡片，卡片上分别标有数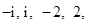其中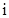是虚数单位．称“从盒中随机抽取一张，记下卡片上的数后并放回”为一次试验（设每次试验的结果互不影响）．
    （1）求事件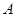 “在一次试验中，得到的数为虚数”的概率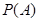与事件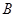 “在四次试验中，
    至少有两次得到虚数” 的概率；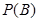
    （2）在两次试验中，记两次得到的数分别为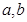，求随机变量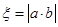的分布列与数学期望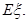

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了解某市市民对政府出台楼市限购令的态度，在该市随机抽取了50名市民进行调查，他们月收入（单位：百元）的频数分布及对楼市限购令的赞成人数如下表：

    月收入

    		[25，35）
    		[35，45）



    频数
    		5
    		10
    		15
    		10
    		5
    		5
    赞成人数
    		4
    		8
    		8
    		5
    		2
    		1
    将月收入不低于55的人群称为“高收入族”，月收入低于55的人群称为“非高收人族”。
    （Ⅰ）根据已知条件完成下面的2×2列联表，有多大的把握认为赞不赞成楼市限购令与收入高低有关？
    已知：，
    当<2.706时，没有充分的证据判定赞不赞成楼市限购令与收入高低有关；
    当>2.706时，有90％的把握判定赞不赞成楼市限购令与收入高低有关；
    当>3.841时，有95％的把握判定赞不赞成楼市限购令与收入高低有关；
    当>6.635时，有99％的把握判定赞不赞成楼市限购令与收入高低有关。
     
    		非高收入族
    		高收入族
    		总计
    赞成
    		 
    		 
    		 
    不赞成
    		 
    		 
    		 
    总计
    		 
    		 
    		 
    （Ⅱ）现从月收入在[55，65）的人群中随机抽取两人，求所抽取的两人中至少一人赞成楼市限购令的概率。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    由于当前学生课业负担较重，造成青少年视力普遍下降，现从某中学随机抽取16名学生，经校医用对数视力表检査得到每个学生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶)如下：
    (I )若视力测试结果不低于5 0，则称为“好视力”，求校医从这16人中随机选取3人，至多有1人是“好视力”的概率；
    (II)以这16人的样本数据来估计整个学校的总体数据，若从该校(人数很多）任选3人，记表示抽到“好视力”学生的人数，求的分布列及数学期望，据此估计该校高中学生（共有5600人）好视力的人数

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知复数z=x+yi(x,y∈R)在复平面上对应的点为M.
    (1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中随机取一个数作为y,求复数z为纯虚数的概率.
    (2)设x∈[0,3],y∈[0,4],求点M落在不等式组:所表示的平面区域内的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某活动将在辽宁沈阳举行，组委会在沈阳某大学招募了12名男志愿者和18名女志愿者，将这30名志愿者的身高编成如图所示的茎叶图(单位：cm)，身高在175 cm以上(包括175 cm)定义为“高个子”，身高在175 cm以下(不包括175 cm)定义为“非高个子”．

    (1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人，再从这5人中选2人，求至少有一人是“高个子”的概率；
    (2)若从身高180 cm以上(包括180 cm)的志愿者中选出男、女各一人，求这2人身高相差5 cm以上的概率．

    查看答案和解析>>

    同步练习册答案