
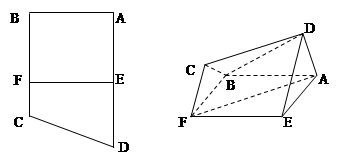
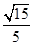
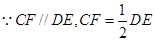 ,所以延长
,所以延长 会相交,
会相交,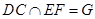 ,则
,则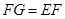 ,
,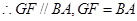 ,
, 是平行四边形,
是平行四边形,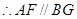 ,又
,又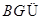 平面
平面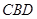
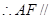 平面
平面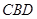 ;……………………6分
;……………………6分 的中点为
的中点为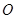 ,
,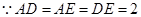 ,则
,则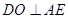 且
且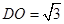 ,
,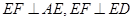 ,
,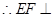 平面
平面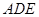 ,
,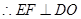 ,
,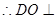 平面
平面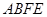 .………………………………………………………………8分
.………………………………………………………………8分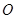 为原点,过点
为原点,过点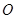 且平行于
且平行于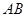 的直线为
的直线为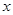 轴,
轴, 所在直线为
所在直线为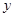 轴,
轴,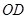 所在直线为
所在直线为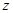 轴,建立空间直角坐标系
轴,建立空间直角坐标系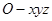 。则平面
。则平面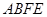 的法向量为
的法向量为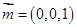 ,点
,点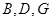 的坐标分别为
的坐标分别为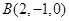 ,
,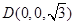 ,
,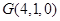 ,………………10分
,………………10分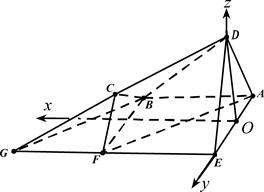
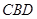 的法向量
的法向量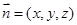 ,则
,则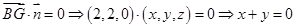 ,
,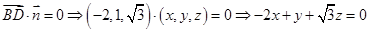
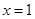 ,则
,则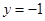 ,
,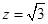 ,即
,即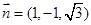 ,
,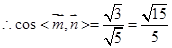 ,
,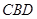 与平面
与平面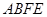 夹角的余弦值为
夹角的余弦值为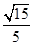 .…………………………………12分
.…………………………………12分

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源:不详 题型:解答题
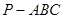 中,
中,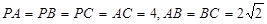
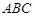 ⊥平面
⊥平面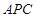
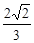 ,求BM的最小值.
,求BM的最小值.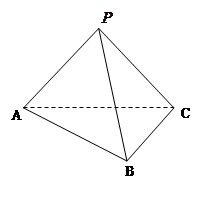
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
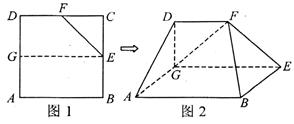
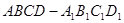 中,
中,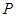 为正方形
为正方形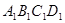 四边上的动点,
四边上的动点,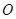 为底面正方形
为底面正方形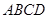 的中心,
的中心,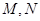 分别为
分别为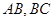 的中点,点
的中点,点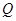 为平面
为平面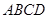 内一点,线段
内一点,线段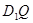 与
与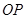 互相平分,则满足
互相平分,则满足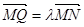 的实数
的实数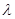 的值有( )
的值有( )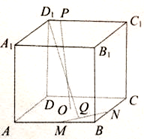
A.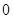 个 个 | B.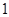 个 个 | C.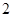 个 个 | D.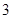 个 个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.底面是正方形,有两个侧面垂直于底面 |
| B.底面是正方形,有两个侧面是矩形 |
| C.底面是菱形,且有一个顶点处的三条棱两两垂直 |
| D.每个底面是全等的矩形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com