
【题目】从抛物线![]() 上任意一点P向x轴作垂线段,垂足为Q,点M是线段
上任意一点P向x轴作垂线段,垂足为Q,点M是线段![]() 上的一点,且满足
上的一点,且满足![]()
(1)求点M的轨迹C的方程;
(2)设直线![]() 与轨迹c交于
与轨迹c交于![]() 两点,T为C上异于
两点,T为C上异于![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】
(1)利用相关点法,设设![]() ,
,![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,由
,由![]() ,从而得到
,从而得到![]() ,即
,即![]() .化简求得结果;
.化简求得结果;
(2)设出点A,B的坐标,将直线与曲线的方程联立,消元得到![]() ,根据韦达定理得到
,根据韦达定理得到![]()
![]() =
=![]() ,
,![]()
![]() =
=![]() ,设点
,设点![]() ,写出直线AT的方程,进而求得点D的坐标,同理求得点E的坐标,如果以
,写出直线AT的方程,进而求得点D的坐标,同理求得点E的坐标,如果以![]() 为直径的圆过
为直径的圆过![]() 轴某一定点
轴某一定点![]() ,则满足
,则满足![]() ,利用向量数量积坐标公式求得结果.
,利用向量数量积坐标公式求得结果.
(1)设![]() ,
,![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .
.
因为![]() ,
,
所以![]() ,
,
即![]() ,
,
因为点![]() 在抛物线
在抛物线![]() 上,
上,
所以![]() ,即
,即![]() .
.
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)解法1:设直线![]() 与曲线
与曲线![]() 的交点坐标为
的交点坐标为![]()
![]() ,
,![]() ,
,
由![]() 得
得![]() .
.
由韦达定理得![]()
![]() =
=![]() ,
,![]()
![]() =
=![]() .
.
设点![]() ,则
,则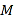 .
.
所以直线![]() 的方程为
的方程为![]() .
.
令![]() ,得点
,得点![]() 的坐标为
的坐标为![]() .
.
同理可得点![]() 的坐标为
的坐标为![]() .
.
如果以![]() 为直径的圆过
为直径的圆过![]() 轴某一定点
轴某一定点![]() ,则满足
,则满足![]() .
.
因为![]()
![]() .
.
所以![]() .
.
即![]() ,解得
,解得![]() 或
或![]() .
.
故以![]() 为直径的圆过
为直径的圆过![]() 轴上的定点
轴上的定点![]() 和
和![]() .
.
解法2:直线![]() 与曲线
与曲线![]() 的交点坐标为
的交点坐标为![]() ,
,![]() ,
,
若取![]() ,则
,则![]() ,
,![]() 与直线
与直线![]() 的交点坐标为
的交点坐标为![]() ,
,![]() ,
,
所以以![]() 为直径的圆的方程为
为直径的圆的方程为![]() .
.
该圆与![]() 轴的交点坐标为
轴的交点坐标为![]() 和
和![]() .
.
所以符合题意的定点只能是![]() 或
或![]() .
.
设直线![]() 与曲线
与曲线![]() 的交点坐标为
的交点坐标为![]()
![]() ,
,![]() ,
,
由![]() 得
得![]() .
.
由韦达定理得![]()
设点![]() ,则
,则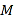 .
.
所以直线![]() 的方程为
的方程为![]() .
.
令![]() ,得点
,得点![]() 的坐标为
的坐标为![]() .
.
同理可得点![]() 的坐标为
的坐标为![]() .
.
若点![]() 满足要求,则满足
满足要求,则满足![]() .
.
因为![]()
![]()
![]() .
.
所以点![]() 满足题意.
满足题意.
同理可证点![]() 也满足题意.
也满足题意.
故以![]() 为直径的圆过
为直径的圆过![]() 轴上的定点
轴上的定点![]() 和
和![]() .
.


科目:高中数学 来源: 题型:
【题目】条件![]()
(1)条件![]() :复数
:复数![]() ,指明
,指明![]() 是
是![]() 的说明条件?若
的说明条件?若![]() 满足条件
满足条件![]() ,记
,记![]() ,求
,求![]()
(2)若上问中![]() ,记
,记![]() 时的
时的![]() 在平面直角坐标系的点
在平面直角坐标系的点![]() 存在过
存在过![]() 点的抛物线
点的抛物线![]() 顶点在原点,对称轴为坐标轴,求抛物线的解析式。
顶点在原点,对称轴为坐标轴,求抛物线的解析式。
(3)自(2)中![]() 点出发的一束光线经抛物线
点出发的一束光线经抛物线![]() 上一点
上一点![]() 反射后沿平行于抛物线
反射后沿平行于抛物线![]() 对称轴方向射出,求:
对称轴方向射出,求:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首项为O的无穷数列![]() 同时满足下面两个条件:
同时满足下面两个条件:
①![]() ;②
;②![]()
(1)请直接写出![]() 的所有可能值;
的所有可能值;
(2)记![]() ,若
,若![]() 对任意
对任意![]() 成立,求
成立,求![]() 的通项公式;
的通项公式;
(3)对于给定的正整数![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,动点![]() 分别与两个定点
分别与两个定点![]() ,
,![]() 的连线的斜率之积为
的连线的斜率之积为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设过点![]() 的直线与轨迹
的直线与轨迹![]() 交于
交于![]() ,
,![]() 两点,判断直线
两点,判断直线![]() 与以线段
与以线段![]() 为直径的圆的位置关系,并说明理由.
为直径的圆的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农户计划种植莴笋和西红柿,种植面积不超过![]() 亩,投入资金不超过
亩,投入资金不超过![]() 万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
年产量/亩 | 年种植成本/亩 | 每吨售价 | |
莴笋 | 5吨 | 1万元 | 0.5万元 |
西红柿 | 4.5吨 | 0.5万元 | 0.4万元 |
那么,该农户一年种植总利润(总利润=总销售收入-总种植成本)的最大值为____万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com