
【题目】已知![]() ,
,![]() 是函数
是函数![]() (其中常数
(其中常数![]() )图象上的两个动点,点
)图象上的两个动点,点![]() ,若
,若![]() 的最小值为0,则函数
的最小值为0,则函数![]() 的最大值为__________.
的最大值为__________.
【答案】![]()
【解析】
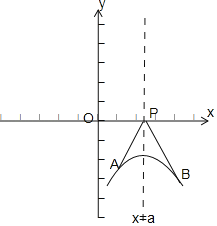
先推出f(x)的图象关于直线x=a对称,然后得出直线PA,PB分别与函数图象相切时,![]()
![]() 的最小值为0,再通过导数的几何意义得切线的斜率,解出a=1,结合图象可得x=1时,f(x)的最大值为
的最小值为0,再通过导数的几何意义得切线的斜率,解出a=1,结合图象可得x=1时,f(x)的最大值为![]() .
.
解:A,B是函数f(x)![]() (其中a>0)图象上的两个动点,
(其中a>0)图象上的两个动点,
当x<a时,f(x)=f(2a﹣x)=﹣e(2a﹣x)﹣2a=﹣e﹣x,
∴函数f(x)的图象关于直线x=a对称.
当点A,B分别位于分段函数的两支上,
且直线PA,PB分别与函数图象相切时,![]()
![]() 的最小值为0,
的最小值为0,
设PA与f(x)=﹣e﹣x相切于点A(x0,y0),
∴f′(x)=e﹣x,∴kAP=f′(x0)=e![]() ,解得x0=a﹣1,
,解得x0=a﹣1,
∵![]()
![]() 的最小值为0,∴
的最小值为0,∴![]() ⊥
⊥![]() ,
,
∴kPA=tan45°=1,∴e![]() 1,∴x0=0,
1,∴x0=0,
∴a=1,∴f(x)max![]() .
.
故答案为:![]()


科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面![]() 底面ABCD,且
底面ABCD,且![]() ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.
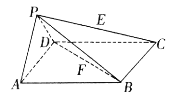
(I)求证:EF//平面PAD;
(II)求三棱锥F-DEC的体积;
(III)在线段CD上是否存在一点G,使得平面![]() 平面PDC?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
平面PDC?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从抛物线![]() 上任意一点P向x轴作垂线段,垂足为Q,点M是线段
上任意一点P向x轴作垂线段,垂足为Q,点M是线段![]() 上的一点,且满足
上的一点,且满足![]()
(1)求点M的轨迹C的方程;
(2)设直线![]() 与轨迹c交于
与轨迹c交于![]() 两点,T为C上异于
两点,T为C上异于![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 和到直线
和到直线![]() 的距离之比为
的距离之比为![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点作垂直于
,过点作垂直于![]() 轴的直线与曲线
轴的直线与曲线![]() 相交于两点,直线
相交于两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 相交于一点(交点位于线段
相交于一点(交点位于线段![]() 上,且与
上,且与![]() 不重合).
不重合).
(1)求曲线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切时,四边形
相切时,四边形![]() 的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高二年级的第二学期,因某学科的任课教师王老师调动工作,于是更换了另一名教师赵老师继任.第二学期结束后从全学年的该门课的学生考试成绩中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如下:
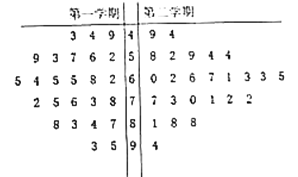
学校秉持均衡发展、素质教育的办学理念,对教师的教学成绩实行绩效考核,绩效考核方案规定:每个学期的学生成绩中与其中位数相差在![]() 范围内(含
范围内(含![]() )的为合格,此时相应的给教师赋分为1分;与中位数之差大于10的为优秀,此时相应的给教师赋分为2分;与中位数之差小于-10的为不合格,此时相应的给教师赋分为-1分.
)的为合格,此时相应的给教师赋分为1分;与中位数之差大于10的为优秀,此时相应的给教师赋分为2分;与中位数之差小于-10的为不合格,此时相应的给教师赋分为-1分.
(Ⅰ)问王老师和赵老师的教学绩效考核平均成绩哪个大?
(Ⅱ)是否有![]() 的把握认为“学生成绩取得优秀与更换老师有关”.
的把握认为“学生成绩取得优秀与更换老师有关”.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农户计划种植莴笋和西红柿,种植面积不超过![]() 亩,投入资金不超过
亩,投入资金不超过![]() 万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
年产量/亩 | 年种植成本/亩 | 每吨售价 | |
莴笋 | 5吨 | 1万元 | 0.5万元 |
西红柿 | 4.5吨 | 0.5万元 | 0.4万元 |
那么,该农户一年种植总利润(总利润=总销售收入-总种植成本)的最大值为____万元
查看答案和解析>>
科目:高中数学 来源: 题型:
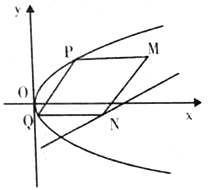
【题目】抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然.如图所示,今有抛物线![]() ,一光源在点
,一光源在点![]() 处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的点
处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的点![]() ,反射后,又射向抛物线上的点
,反射后,又射向抛物线上的点![]() ,再反射后又沿平行于抛物线的对称轴方向射出,途中遇到直线
,再反射后又沿平行于抛物线的对称轴方向射出,途中遇到直线![]() 上的
上的![]() 点,再反射后又射回点
点,再反射后又射回点![]() .设
.设![]() ,
,![]() 两点的坐标分别是
两点的坐标分别是![]() ,
,![]() .
.
(1)证明:![]() ;
;
(2)若四边形![]() 是平行四边形,且点
是平行四边形,且点![]() 的坐标为
的坐标为![]() .求直线
.求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知![]() ,且2an+1=an+1(n∈N*).
,且2an+1=an+1(n∈N*).
(1)求证:数列{an-1}是等比数列;
(2)若bn=nan,求数列{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com