
【题目】在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
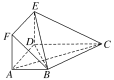
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
【答案】见解析
【解析】解:(1)证明:因为AD=1,CD=2,AC=![]() ,
,
所以AD2+CD2=AC2,
所以△ADC为直角三角形,且AD⊥DC.
同理,因为ED=1,CD=2,EC=![]() ,
,
所以ED2+CD2=EC2,
所以△EDC为直角三角形,且ED⊥DC.
又四边形ADEF是正方形,所以AD⊥DE,
又AD∩DC=D,所以ED⊥平面ABCD.
又BC平面ABCD,所以ED⊥BC.
在梯形ABCD中,过点B作BH⊥CD于点H,

故四边形ABHD是正方形,所以∠ADB=45°,BD=![]() 。
。
在Rt△BCH中,BH=CH=1,所以BC=![]() ,
,
故BD2+BC2=DC2,所以BC⊥BD.
因为BD∩ED=D,BD平面EBD,ED平面EBD,
所以BC⊥平面EBD,
又BC平面EBC,所以平面EBC⊥平面EBD.
(2)在线段BC上存在一点T,使得MT∥平面BDE,此时3BT=BC.
连接MT,在△EBC中,因为![]() =
=![]() =
=![]() ,所以MT∥EB.
,所以MT∥EB.
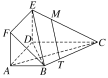
又MT平面BDE,EB平面BDE,
所以MT∥平面BDE。


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列{n∈N+}.
求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+![]() 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0, ![]() ]上是减函数,在[
]上是减函数,在[![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)已知f(x)=![]() ,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=-x-2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把1、2、3、4、5这五个数字组成无重复数字的五位数,并把它们由小大到的顺序排成一个数列.
(Ⅰ)求![]() 是这个数列的第几项;
是这个数列的第几项;
(Ⅱ)求这个数列的第96项;
(Ⅲ)求这个数列的所有项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的图象如图所示,曲线BCD为抛物线的一部分.
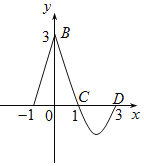
(Ⅰ)求f(x)解析式;
(Ⅱ)若f(x)=1,求x的值;
(Ⅲ)若f(x)>f(2-x),求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com