
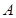 、
、 、
、 、
、 、
、 ,它的一个面
,它的一个面 内接于⊙
内接于⊙ ,
, 是⊙
是⊙ 的直径,四边形
的直径,四边形 为平行四边形,
为平行四边形, 平面
平面 .
.
 平面
平面 ;
; ,
, ,
, ,求该简单几何体的体积.
,求该简单几何体的体积.
 平面
平面
 平面
平面 ,
, 平面
平面 ,
, . ………1分
. ………1分 是⊙
是⊙ 的直径,
的直径,
 , ………2分
, ………2分 ………3分
………3分 平面
平面 , ………4分
, ………4分
 平面
平面 ………5分
………5分 平面
平面 ………6分
………6分 平面
平面
 平面
平面 . ………7分
. ………7分 ,
,
 平面
平面
 平面
平面
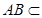 平面
平面


 中
中

 ………8分
………8分 ,由(1),(2)知
,由(1),(2)知 是三棱锥
是三棱锥 的高,
的高, 是三棱锥
是三棱锥 的高
的高 ………9分
………9分 ………11分
………11分 ………13分
………13分 该简单组合体的体积
该简单组合体的体积 . ………14分
. ………14分 平面
平面 ,
,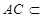 平面
平面 ,
, .
.  ,
, 
 平面
平面 ,
,  是四棱锥
是四棱锥 的高,且由(1),(2)证明易知四边形
的高,且由(1),(2)证明易知四边形 为边长为
为边长为 的正方形. ………10分
的正方形. ………10分 ………11分
………11分 ………12分
………12分 ………13分
………13分
 ………14分
………14分

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com