练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    圆与x轴的正半轴交于点B，Q是圆上异于原点的任一点，过B点的切线与OQ的延长线相交于点A．在射线OQ上取一点P，使|OP|＝|QA|．求P点轨迹的一个参数方程，并把它化为普通方程．

    答案：
    解析：

    解：设∠BOA＝θ，取θ为参数，则－＜θ＜．连结QB．则|OQ|＝cosθ，|OA|＝secθ，∴|QA|＝|OA|－|OQ|＝secθ－cosθ＝|OP|．设P(x，y)，根据三角函数的定义，x＝|QA|cosθ＝θ，y＝|QA|sinθ＝，∴，∴＝0．∴P点轨迹的一个参数方程为(θ为参数，－＜θ＜)，它的普通方程为＝0(0≤x＜1)．


    提示：

    说明：求P点的一个轨迹方程，关键在于选择适当的参数，可以简化解题过程，在化普通方程的过程中用了平方运算，由于对称性，故没有扩大范围．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在平面直角坐标系xOy中，角α，β (0＜α＜
    π
    2
    ， 
    π
    2
    ＜β＜π)    的顶点与原点O重合，始边与x轴的正半轴重合，终边分别与单位圆交于A，B两点，A，B两点的纵坐标分别为
    5
    13
    ，
    3
    5
    ．
    （Ⅰ）求tanβ的值；
    （Ⅱ）求△AOB的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，圆x2+y2=4与y轴的正半轴交于点B，P是圆上的动点，P点在x轴上的投影是D，点M满足
    DM
    =
    1
    2
    DP
    ．
    （1）求动点M的轨迹C的方程，并说明轨迹是什么图形．
    （2）过点B的直线l与M点的轨迹C交于不同的两点E、F，若
    BF
    =2
    BE
    ，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

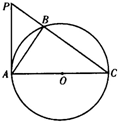    （二）选择题（考生在A、B、C三小题中选做一题，多做按所做第一题评分）
    A．（不等式选讲） 函数f(x)=
    		|x-2|-1
    的定义域为
    （-∞，1]∪[3，+∞）
    （-∞，1]∪[3，+∞）

    B．（坐标系与参数方程）已知极点在直角坐标系的原点O处，极轴与x轴的正半轴重合，曲线C的极坐标方程为ρ=2cosθ，直线l的参数方程为
    x=
    3
    5
    t
    y=1+
    4
    5
    t
    （t为参数）．则曲线C上的点到直线l的最短距离为
    2
    5
    2
    5
    ．
    C．（几何证明选讲）如图，PA是圆O的切线，切点为A，PA=2．AC是圆O的直径，PC与圆O交于B，PB=1，则AC=
    2
    		3
    2
    		3
    ．

    查看答案和解析>>

    科目：高中数学 来源：吉林省延边州2012届高三下学期复习质量检测数学文科试题 题型：044

    已知点A(0，－1)在椭圆G：(a＞b＞0)上，设椭圆G与x轴的正半轴的交点为B，其右焦点为F，且∠AFB＝，过x轴上一点M(m，0)作一条不垂直于y轴的直线l交椭圆G于C，D两点．

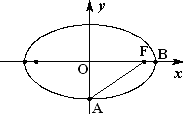
    (Ⅰ)求椭圆G的方程；

    (Ⅱ)以CD为直径的圆恒过B点，求实数m的值．

    查看答案和解析>>

    同步练习册答案