
 .
.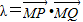 .求λ的取值范围;
.求λ的取值范围; ,把1换成0,就得到它的渐近线方程.
,把1换成0,就得到它的渐近线方程. ,然后运用向量数量积的坐标运算能够求出λ的取值范围.
,然后运用向量数量积的坐标运算能够求出λ的取值范围.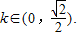 再由题设条件根据k的不同取值范围试将s表示为直线l的斜率k的函数.
再由题设条件根据k的不同取值范围试将s表示为直线l的斜率k的函数.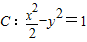 ,把1换成0,
,把1换成0,
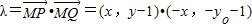 =
=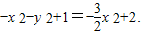
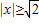
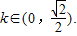
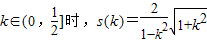 ;
;



科目:高中数学 来源: 题型:
(08年上海卷文)(本题满分16分)已知双曲线![]() .
.
(1)求双曲线![]() 的渐近线方程;
的渐近线方程;
(2)已知点![]() 的坐标为
的坐标为![]() .设
.设![]() 是双曲线
是双曲线![]() 上的点,
上的点,![]() 是点
是点![]() 关于原点的对称点.
关于原点的对称点.
记![]() .求
.求![]() 的取值范围;
的取值范围;
(3)已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() 为双曲线
为双曲线![]() 上在第一象限内的点.记
上在第一象限内的点.记![]() 为经过原点与点
为经过原点与点![]() 的直线,
的直线,![]() 为
为![]() 截直线
截直线![]() 所得线段的长.试将
所得线段的长.试将![]() 表示为直线
表示为直线![]() 的斜率
的斜率![]() 的函数.
的函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分6分,
第3小题满分7分.
已知双曲线![]() .
.
(1)求双曲线![]() 的渐近线方程;
的渐近线方程;
(2)已知点![]() 的坐标为
的坐标为![]() .设
.设![]() 是双曲线
是双曲线![]() 上的点,
上的点,![]() 是点
是点![]() 关于原点的对称点.
关于原点的对称点.
记![]() .求
.求![]() 的取值范围;
的取值范围;
(3)已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() 为双曲线
为双曲线![]() 上在第一象限内的点.记
上在第一象限内的点.记![]() 为经过原点与点
为经过原点与点![]() 的直线,
的直线,![]() 为
为![]() 截直线
截直线![]() 所得线段的长.试将
所得线段的长.试将![]() 表示为直线
表示为直线![]() 的斜率
的斜率![]() 的函数.
的函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线![]() .
.
(1)求双曲线![]() 的渐近线方程;
的渐近线方程;
(2)已知点![]() 的坐标为
的坐标为![]() .设
.设![]() 是双曲线
是双曲线![]() 上的点,
上的点,![]() 是点
是点![]() 关于原点的对称点.
关于原点的对称点.
记![]() .求
.求![]() 的取值范围;
的取值范围;
(3)已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() 为双曲线
为双曲线![]() 上在第一象限内的点.记
上在第一象限内的点.记![]() 为经过原点与点
为经过原点与点![]() 的直线,
的直线,![]() 为
为![]() 截直线
截直线![]() 所得线段的长.试将
所得线段的长.试将![]() 表示为直线
表示为直线![]() 的斜率
的斜率![]() 的函数.
的函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
(上海卷文20)已知双曲线![]() .
.
(1)求双曲线![]() 的渐近线方程;
的渐近线方程;
(2)已知点![]() 的坐标为
的坐标为![]() .设
.设![]() 是双曲线
是双曲线![]() 上的点,
上的点,![]() 是点
是点![]() 关于原点的对称点.
关于原点的对称点.
记![]() .求
.求![]() 的取值范围;
的取值范围;
(3)已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() 为双曲线
为双曲线![]() 上在第一象限内的点.记
上在第一象限内的点.记![]() 为经过原点与点
为经过原点与点![]() 的直线,
的直线,![]() 为
为![]() 截直线
截直线![]() 所得线段的长.试将
所得线段的长.试将![]() 表示为直线
表示为直线![]() 的斜率
的斜率![]() 的函数.
的函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com