
 ,和x
,和x 分别解不等式组即可.
分别解不等式组即可.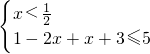 或
或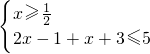 ,
,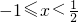 或
或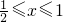 ,即-1≤x≤1.
,即-1≤x≤1.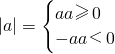 ,就可结合分类讨论思想,将不等式进行等价转化,轻松完成此题的解答.《不等式选讲》这一专题,以基本不等式、绝对值不等式、柯西不等式作为命题的热点,离不开必修部分《不等式》章节的扎实基础.
,就可结合分类讨论思想,将不等式进行等价转化,轻松完成此题的解答.《不等式选讲》这一专题,以基本不等式、绝对值不等式、柯西不等式作为命题的热点,离不开必修部分《不等式》章节的扎实基础. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| 4 |
| b |
| a |
| b |
| a |
| b |
| b |
| 7π |
| 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com