
当 时
时 ,
,

(1)求
(2)猜想 与
与 的关系,并用数学归纳法证明。
的关系,并用数学归纳法证明。
(1) ,
, ,
, ,
,
(2) =
= ,理由见解析
,理由见解析
【解析】
试题分析:解:(1) ,
,
 ,
,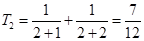
(2)猜想: 即:
即:
 (n∈N*)
(n∈N*)
下面用数学归纳法证明
n=1时,已证S1=T1
假设n=k时,Sk=Tk(k≥1,k∈N*),即:

则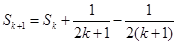





由①,②可知,对任意n∈N*,Sn=Tn都成立.
考点:数学归纳法
点评:本题用到的数学归纳法,在高中数学中常用来证明等式成立和数列通项公式成立。若要证明一个与自然数n有关的命题P(n),有如下步骤:
(1)证明当n取第一个值 时命题成立。
时命题成立。 对于一般数列取值为0或1,但也有特殊情况;
对于一般数列取值为0或1,但也有特殊情况;
(2)假设当n=k(k≥ ,k为自然数)时命题成立,证明当n=k+1时命题也成立。
,k为自然数)时命题成立,证明当n=k+1时命题也成立。
综合(1)(2),对一切自然数n(≥ ),命题P(n)都成立。
),命题P(n)都成立。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届山东省高一上学期期中调研数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当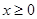 时,
时,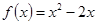 .
.
(1)求当 时,
时, 的解析式;
的解析式;
(2)作出函数 的图象,并指出其单调区间(不必证明).
的图象,并指出其单调区间(不必证明).
查看答案和解析>>
科目:高中数学 来源:江西省09-10学年高二下学期第二次段考数学文科试卷 题型:填空题
(12分)已知函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,
(1)求 的解析式;
的解析式;
(2)讨论函数 的单调性,并求
的单调性,并求 的值域。
的值域。
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一上学期期中数学试题 题型:填空题
(本小题满分14分)
f(x)是定义在R上的奇函数,且 ,当
,当 时,
时,
(1)求函数 的周期 (2)求函数
的周期 (2)求函数 在
在 的表达式
(3)求
的表达式
(3)求
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com