
【题目】已知函数f(x)=(m+2cos2x)cos(2x+θ)为奇函数,且f( ![]() )=0,其中m∈R,θ∈(0,π)
)=0,其中m∈R,θ∈(0,π)
(Ⅰ)求函数f(x)的图象的对称中心和单调递增区间
(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,且f( ![]() +
+ ![]() )=﹣
)=﹣ ![]() ,c=1,ab=2
,c=1,ab=2 ![]() ,求△ABC的周长.
,求△ABC的周长.
【答案】解:(Ⅰ)f( ![]() )=﹣(m+1)sinθ=0,
)=﹣(m+1)sinθ=0,
∵θ∈(0,π).
∴sinθ≠0,
∴m+1=0,即m=﹣1,
∵f(x)为奇函数,
∴f(0)=(m+2)cosθ=0,
∴cosθ=0,θ= ![]() .
.
故f(x)=(﹣1+2cos2x)cos(2x+ ![]() )=cos2x(﹣sin2x)=﹣
)=cos2x(﹣sin2x)=﹣ ![]() sin4x,
sin4x,
由4x=kπ,k∈Z得:x= ![]() kπ,k∈Z,
kπ,k∈Z,
故函数f(x)的图象的对称中心坐标为:( ![]() kπ,0),k∈Z,
kπ,0),k∈Z,
由4x∈[ ![]() +2kπ,
+2kπ, ![]() +2kπ],k∈Z得:x∈[
+2kπ],k∈Z得:x∈[ ![]() +
+ ![]() kπ,
kπ, ![]() +
+ ![]() kπ],k∈Z,
kπ],k∈Z,
即函数f(x)的单调递增区间为[ ![]() +
+ ![]() kπ,
kπ, ![]() +
+ ![]() kπ],k∈Z,
kπ],k∈Z,
(Ⅱ)∵f( ![]() +
+ ![]() )=﹣
)=﹣ ![]() sin(2C+
sin(2C+ ![]() )﹣
)﹣ ![]() ,C为三角形内角,
,C为三角形内角,
故C= ![]() ,
,
∴c2=a2+b2﹣2abcosC= ![]() =
= ![]() ,
,
∵c=1,ab=2 ![]() span> ,
span> ,
∴a+b=2+ ![]() ,
,
∴a+b+c=3+ ![]() ,
,
即△ABC的周长为3+ ![]()
【解析】(Ⅰ)把x=![]() 代入函数解析式可求得m的值,进而根据函数为奇函数推断出f(0)=0,进而求得cosθ,则θ的值可得函数解析式,进而可得函数f(x)的图象的对称中心和单调递增区间(Ⅱ)由f(
代入函数解析式可求得m的值,进而根据函数为奇函数推断出f(0)=0,进而求得cosθ,则θ的值可得函数解析式,进而可得函数f(x)的图象的对称中心和单调递增区间(Ⅱ)由f(![]() +
+![]() )=﹣
)=﹣![]() 可得C角,结合余弦定理及c=1,ab=2
可得C角,结合余弦定理及c=1,ab=2![]() ,可得△ABC的周长.
,可得△ABC的周长.
【考点精析】解答此题的关键在于理解函数的奇函数的相关知识,掌握一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=—f(x),那么f(x)就叫做奇函数,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinωx cosωx﹣sin2ωx+1(ω>0)相邻两条对称轴之间的距离为
sinωx cosωx﹣sin2ωx+1(ω>0)相邻两条对称轴之间的距离为 ![]() .
.
(Ⅰ)求ω的值及函数f(x)的单调递减区间;
(Ⅱ)已知a,b,c分别为△ABC中角A,B,C的对边,且满足a= ![]() ,f(A)=1,求△ABC 面积 S 的最大值.
,f(A)=1,求△ABC 面积 S 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1(a>0,b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,P是双曲线在第一象限上的点且满足|PF1|=2|PF2|,直线PF2交双曲线C于另一点N,又点M满足
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,P是双曲线在第一象限上的点且满足|PF1|=2|PF2|,直线PF2交双曲线C于另一点N,又点M满足 ![]() =
= ![]() 且∠MF2N=120°,则双曲线C的离心率为( )
且∠MF2N=120°,则双曲线C的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= ![]() AD=1,CD=
AD=1,CD= ![]() .
. 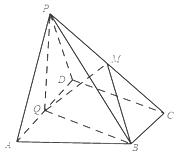
(1)求证:平面MQB⊥平面PAD;
(2)若二面角M﹣BQ﹣C大小的为60°,求QM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程ρ=2cosθ,直线l的参数方程是 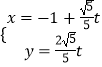 (t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)设直线l与y轴的交点是M,N是曲线C上一动点,求|MN|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a、b、c是角A、B、C的对边,则下列结论正确的序号是 . ①若a、b、c成等差数列,则B= ![]() ; ②若c=4,b=2
; ②若c=4,b=2 ![]() ,B=
,B= ![]() ,则△ABC有两解;
,则△ABC有两解;
③若B= ![]() ,b=1,ac=2
,b=1,ac=2 ![]() ,则a+c=2+
,则a+c=2+ ![]() ; ④若(2c﹣b)cosA=acosB,则A=
; ④若(2c﹣b)cosA=acosB,则A= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣ ![]() |﹣|2x+1|. (Ⅰ)求f(x)的值域;
|﹣|2x+1|. (Ⅰ)求f(x)的值域;
(Ⅱ)若f(x)的最大值时a,已知x,y,z均为正实数,且x+y+z=a,求证: ![]() +
+ ![]() +
+ ![]() ≥1.
≥1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移 ![]() 个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
A.关于点( ![]() ,0)对称?
,0)对称?
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称?
,0)对称?
D.关于直线x= ![]() 对称
对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com