
(本题满分14分)
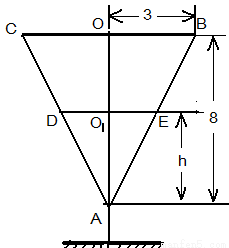
如图,酒杯的形状为倒立的圆锥,杯深8 cm .上口宽6cm , 水以20 cm3/s的流量倒入杯中,当水深为4 cm时,求水升高的瞬时变化率.

解法一:设时刻t s时,杯中水的体积为Vcm3,水面半径为r cm, 水深为h cm.
则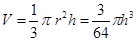 2分
2分
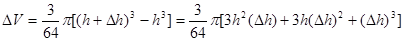 5分
5分
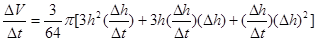 7分
7分
记水升高的瞬时变化率为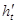 (即当
(即当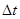 无限趋近于0时,
无限趋近于0时,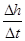 无限趋近于
无限趋近于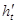 )
)
从而有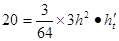 ,当h=4时,解得
,当h=4时,解得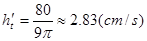 12分
12分
答:当水深为4 cm时,水升高的瞬时变化率为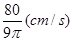 。
14分
。
14分
解法二:仿解法一,可得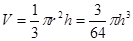 ,即
,即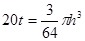 4分
4分
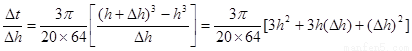 5分
5分
当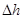 无限趋近于0时,
无限趋近于0时,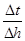 无限趋近于
无限趋近于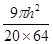 ,即
,即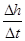 无限趋近于
无限趋近于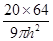 12分
12分
当h=4时,水升高的瞬时变化率是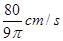 .
14分
.
14分
解法三:水面高为4 cm时,可求得水面半径为 ,设水面高度增加
,设水面高度增加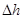 时,水的体积增加
时,水的体积增加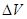 ,从而
,从而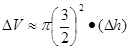 ,(用圆柱近似增加的水体积) ,
8分
,(用圆柱近似增加的水体积) ,
8分
故 .当
.当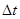 无限趋近于0时得
无限趋近于0时得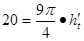 10分
10分
即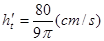 12分
12分
答:当水深为4 cm时,水升高的瞬时变化率为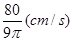 。
14分
。
14分
解法四:设t 时刻时注入杯中的水的高度为 h ,杯中水面为圆形,其圆半径为r 1分
如图被子的轴截面为等腰三角形ABC,AO1O为底边BC上的高,O1,O 分别为DE,BC中点,
容易求证 ∽
∽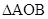 ,那么
,那么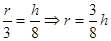 2分
2分
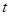 时刻时杯中水的容积为V=
时刻时杯中水的容积为V=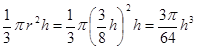 3分
3分
又因为V=20t, 4分
 则
则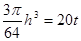 即
即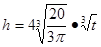 6分
6分
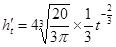 8分
8分
当h=4 时,设t=t1,
由三角形形似的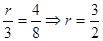 ,
9分
,
9分
那么
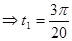 10分
10分
答:当水高为4 cm时,水升高的瞬时变化率为 cm/s
14分
cm/s
14分
【解析】略


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,![]() 为
为![]() 上的点,且BF⊥平面ACE.
上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;(2)求三棱锥D-AEC的体积;(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三上学期期中考试数学 题型:解答题
(本题满分14分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}
(Ⅰ)若A B=[0,3],求实数m的值
B=[0,3],求实数m的值
(Ⅱ)若A CRB,求实数m的取值范围
CRB,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三上学期第三次月考理科数学卷 题型:解答题
(本题满分14分)
已知点 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 作
作 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。
(1)求动点 的轨迹方程;
的轨迹方程;
(2)已知点 ,在动点
,在动点 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2014届江西省高一第二学期入学考试数学 题型:解答题
(本题满分14分)已知函数 .
.
(1)求函数 的定义域;
的定义域;
(2)判断 的奇偶性;
的奇偶性;
(3)方程 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使

 ;如果没有,请说明理由?(注:区间的长度为
;如果没有,请说明理由?(注:区间的长度为 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com