
(满分12分) 已知函数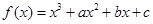 在
在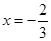 与
与 时都取得极值
时都取得极值
(1)求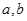 的值与函数
的值与函数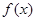 的单调区间
的单调区间
(2)若对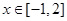 ,不等式
,不等式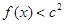 恒成立,求c的取值范围
恒成立,求c的取值范围
科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2012届湖南省澧县一中、岳阳县一中高三11月联考理科数学 题型:解答题
(本小题满分12分)
已知锐角△ABC的三内角A、B、C的对边分别是a、b、c,且(b2+c2-a2)tanA= bc.
bc.
(1)求角A的大小;
(2)求sin(A+10°)·[1- tan(A-10°)]的值.
tan(A-10°)]的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年吉林省长春外国语学校高二下学期期末考试文数 题型:解答题
(本小题满分12分)
已知椭圆C: (常数
(常数 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右
顶点,定点A的坐标为(2,0).
(1)若M与A重合,求曲线C的焦点坐标.
(2)若 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值.
(3)若|PA|最小值为|MA|,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁沈阳二中等重点中学协作体高三领航高考预测(四)理数学卷(解析版) 题型:解答题
(本小题满分12分)已知函数 ,
,
(1)若 时,
时, 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围;
(2)设函数 的图象
的图象 与函数
与函数 的图象
的图象 交于
交于 ,
, 两点,过线段
两点,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 于点
于点 ,
, ,问是否存在点
,问是否存在点 ,使
,使 在
在 处的切线与
处的切线与 在
在 处的切线平行?若存在,求
处的切线平行?若存在,求 的横坐标,若不存在,请说明理由。
的横坐标,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com