
 ,根据a∈(0,1)可求得M的取值范围,从而可求得M的整数部分,继而得到答案.
,根据a∈(0,1)可求得M的取值范围,从而可求得M的整数部分,继而得到答案. ,a∈(0,1)
,a∈(0,1) ,t∈(1,2).
,t∈(1,2). 在(1,
在(1,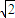 ]上单调递减,在[
]上单调递减,在[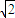 ,2)上单调递增,
,2)上单调递增, +
+ =2
=2 ,当t=1或t=2,M=3,
,当t=1或t=2,M=3, ≤M<3.
≤M<3. (由于t∈(1,2),在这里是“单钩“)”性质的掌握与应用,属于中档题.
(由于t∈(1,2),在这里是“单钩“)”性质的掌握与应用,属于中档题. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com