练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    曲线y1＝2－x2与y2＝x3－2(x＞0)在交点处切线的夹角是_________(以弧度作答)

    答案：
    解析：

    　　答案：

    　　解析：先求出曲线的交点横坐标，然后求函数的导函数，再求切线的斜率，最后用夹角公式求出夹角．

    　　联立求得交点横坐标x1＝2，x2＝－2，x3＝－4(舍负)

    　　由y1＝2－2得1＝－x

    　　由y2＝x3－2得2＝x2

    　　当x1＝2，则k1＝－2，k2＝3，tanα＝||＝1

    　　所以两条切线的夹角为．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：高中数学全解题库(国标苏教版·必修4、必修5) 苏教版 题型：044

    设P0(x0，y0)为曲线C：y＝x2(x＞0)上的点，过P0作曲线C的切线与x轴交于点Q1，过Ql作平行于y轴的直线与曲线C交于点P1(xl，y1)，然后再过P1作曲线C的切线交x轴于点Q2，过Q2作平行于y轴的直线与曲线C交于点P2(x2，y2)，依此类推，作出以下各点：P0，Q1，P1，Q2，P2，Q3，…，Pn，Qn+l，…．已知x0＝2，设Pn坐标为(xn，yn)(n∈N)．

    (1)求出过点P0的切线的方程；

    (2)设xn＝f(n)，求f(n)的表达式．

    查看答案和解析>>

    科目：高中数学 来源：南通高考密卷·数学（理） 题型：044

    设C：y＝x2(x＞0)上的点为P0(x0，y0)，过P0作曲线C的切线与x轴交于Q1，过Q1作平行于y轴的直线与曲线C交于P1(x1，y1)，然后再过P1作曲线C的切线与x轴交于Q2，过Q2作平行于y轴的直线与曲线C交于P2(x2，y2)，依次类推，作出以下各点：Q3，P3，…，Pn，Qn+1，…．已知x0＝2，设Pn(xn，yn)(n∈N)．

    (1)设xn＝f(n)，求f(n)的表达式；

    (2)求g(n)＝；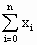

    (3)设Sn＝[g(n)－4]log2f(n)．若n＞2，求证：－1≤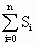＜0．

    查看答案和解析>>

    科目：高中数学 来源：2008年高考预测卷数学科(一)新课标 题型：013

    已知函数y＝x3＋x2＋x的图像C上存在一定点P满足：若过点p的直线l与曲线C交于不同于P的两点M(x1，y1)，N(x2，y2)，就恒有y1＋y2为定值y0，则y0的值为

    [　　]

    A．－

    B．－

    C．－

    D．－2

    查看答案和解析>>

    科目：高中数学 来源：福建省师大附中2012届高三高考模拟数学理科试题 题型：044

    如下图，过曲线C：y＝ex上一点P0(0，1)作曲线C的切线l0交x轴于点Q1(x1，0)，又过Q1作x轴的垂线交曲线C于点P1(x1，y1)，然后再过P1(x1，y1)作曲线C的切线l1交x轴于点Q2(x2，0)，又过Q2作x轴的垂线交曲线C于点P2(x2，y2)，…，以此类推，过点Pn的切线ln与x轴相交于点Qn+1(xn+1，0)，再过点Qn+1作x轴的垂线交曲线C于点Pn+1(xn+1，yn+1)(n∈N*)．

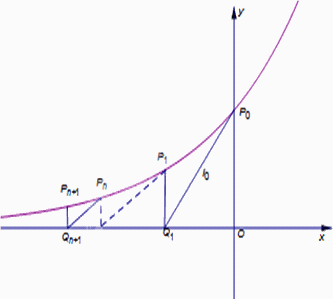
    (1)求x1、x2及数列{xn}的通项公式；

    (2)设曲线C与切线ln及直线Pn+1Qn+1所围成的图形面积为Sn，求Sn的表达式；(3)在满足(2)的条件下，若数列{Sn}的前n项和为Tn，求证：N*．

    查看答案和解析>>

    同步练习册答案