
【题目】将函数f(x)=sin 3x-![]() cos 3x+1的图象向左平移
cos 3x+1的图象向左平移![]() 个单位长度,得到函数g(x)的图象,给出下列关于g(x)的结论:
个单位长度,得到函数g(x)的图象,给出下列关于g(x)的结论:
①它的图象关于直线x=![]() 对称;
对称;
②它的最小正周期为![]() ;
;
③它的图象关于点(![]() ,1)对称;
,1)对称;
④它在[![]() ]上单调递增.
]上单调递增.
其中所有正确结论的编号是( )
A.①②B.②③C.①②④D.②③④
【答案】B
【解析】
根据函数![]() 图象的平移变换公式求出函数
图象的平移变换公式求出函数![]() 的解析式,再利用正弦函数的对称性、单调区间等相关性质求解即可.
的解析式,再利用正弦函数的对称性、单调区间等相关性质求解即可.
因为f(x)=sin 3x-![]() cos 3x+1=2sin(3x-
cos 3x+1=2sin(3x-![]() )+1,由
)+1,由![]() 图象的平移变换公式知,
图象的平移变换公式知,
函数g(x)=2sin[3(x+![]() )-
)-![]() ]+1=2sin(3x+
]+1=2sin(3x+![]() )+1,其最小正周期为
)+1,其最小正周期为![]() ,故②正确;
,故②正确;
令3x+![]() =kπ+
=kπ+![]() ,得x=
,得x=![]() +
+![]() (k∈Z),所以x=
(k∈Z),所以x=![]() 不是对称轴,故①错误;
不是对称轴,故①错误;
令3x+![]() =kπ,得x=
=kπ,得x=![]() -
-![]() (k∈Z),取k=2,得x=
(k∈Z),取k=2,得x=![]() ,故函数g(x)的图象关于点(
,故函数g(x)的图象关于点(![]() ,1)对称,故③正确;
,1)对称,故③正确;
令2kπ-![]() ≤3x+
≤3x+![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,得
,k∈Z,得![]() -
-![]() ≤x≤
≤x≤![]() +
+![]() ,取k=2,得
,取k=2,得![]() ≤x≤
≤x≤![]() ,取k=3,得
,取k=3,得![]() ≤x≤
≤x≤![]() ,故④错误;
,故④错误;
故选:B


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】如图1,![]() 与
与![]() 是处在同-个平面内的两个全等的直角三角形,
是处在同-个平面内的两个全等的直角三角形,![]()
![]() ,
,![]() ,连接是
,连接是![]() 边
边![]() 上一点,过
上一点,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,沿
,沿![]() 将
将![]() 向上翻折,得到如图2所示的六面体
向上翻折,得到如图2所示的六面体![]()
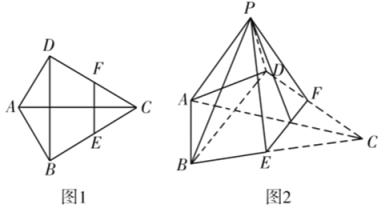
(1)求证:![]()
(2)设![]() 若平面
若平面![]() 底面
底面![]() ,若平面
,若平面![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() ,求
,求![]() 的值;
的值;
(3)若平面![]() 底面
底面![]() ,求六面体
,求六面体![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】移动支付(支付宝支付,微信支付等)开创了新的支付方式,使电子货币开始普及,为了了解习惯使用移动支付方式是否与年龄有关,对某地200人进行了问卷调查,得到数据如下:60岁以上的人群中,习惯使用移动支付的人数为30人;60岁及以下的人群中,不习惯使用移动支付的人数为40人.已知在全部200人中,随机抽取一人,抽到习惯使用移动支付的人的概率为0.6.
(1)完成如下的列联表,并判断是否有![]() 的把握认为习惯使用移动支付与年龄有关,并说明理由.
的把握认为习惯使用移动支付与年龄有关,并说明理由.
习惯使用移动支付 | 不习惯使用移动支付 | 合计(人数) | |
60岁以上 | |||
60岁及以下 | |||
合计(人数) | 200 |
(2)在习惯使用移动支付的60岁以上的人群中,每月移动支付的金额如下表:
每月支付金额 |
|
| 300以上 |
人数 | 15 |
| 5 |
现采用分层抽样的方法从中抽取6人,再从这6人中随机抽取2人,求这2人中有1人月支付金额超过3000元的概率.
附: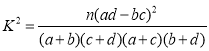 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的右顶点与抛物线
)的右顶点与抛物线![]() :
:![]() (
(![]() )的焦点重合.
)的焦点重合.![]() 的离心率为
的离心率为![]() ,过
,过![]() 的右焦点F且垂直于x轴的直线截
的右焦点F且垂直于x轴的直线截![]() 所得的弦长为
所得的弦长为![]() .
.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线l与椭圆
的直线l与椭圆![]() 交于A,B两点,点B关于x轴的对称点为点E,证明:直线
交于A,B两点,点B关于x轴的对称点为点E,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).设
).设![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( )
①已知函数![]() 是一次函数,若数列
是一次函数,若数列![]() 通项公式为
通项公式为![]() ,则该数列是等差数列;
,则该数列是等差数列;
②若直线![]() 上有两个不同的点到平面
上有两个不同的点到平面![]() 的距离相等,则
的距离相等,则![]() ;
;
③在![]() 中,“
中,“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
④若![]() ,则
,则![]() 的最大值为2.
的最大值为2.
A.1B.2C.3D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】惠州市某商店销售某海鲜,经理统计了春节前后50天该海鲜的日需求量![]() (
(![]() ,单位:公斤),其频率分布直方图如下图所示.该海鲜每天进货1次,每销售1公斤可获利40元;若供大于求,剩余的海鲜削价处理,削价处理的海鲜每公斤亏损10元;若供不应求,可从其它商店调拨,调拨的海鲜销售1公斤可获利30元.假设商店该海鲜每天的进货量为14公斤,商店销售该海鲜的日利润为
,单位:公斤),其频率分布直方图如下图所示.该海鲜每天进货1次,每销售1公斤可获利40元;若供大于求,剩余的海鲜削价处理,削价处理的海鲜每公斤亏损10元;若供不应求,可从其它商店调拨,调拨的海鲜销售1公斤可获利30元.假设商店该海鲜每天的进货量为14公斤,商店销售该海鲜的日利润为![]() 元.
元.
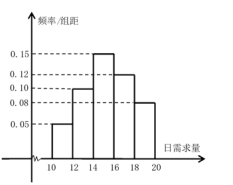
(1)求商店日利润![]() 关于日需求量
关于日需求量![]() 的函数表达式.
的函数表达式.
(2)根据频率分布直方图,
①估计这50天此商店该海鲜日需求量的平均数.
②假设用事件发生的频率估计概率,请估计日利润不少于620元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com