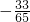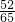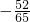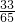B
分析:根据α与β的范围,求出α+β的范围,然后根据角的范围分别利用同角三角函数间的基本关系求出cos(α+β)和sinβ的值,把α变为(α+β)-β,然后利用两角差的余弦函数公式化简后,把各项的值代入即可求出.
解答:因为α∈(0,

),β∈(

,π),
所以α+β∈(

,

),
则cos(α+β)=-
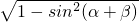
=-

,sinβ=
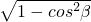
=

,
所以cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ=(-

)×(-

)+

×
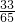
=
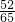
故选B
点评:考查学生灵活运用同角三角函数间的基本关系化简求值,做题时应注意角的变换及角的范围.

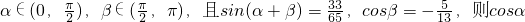 的值是
的值是