
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y(单位:升)关于行驶速度x(单位:千米/时)的函数解析式可以表示为:y=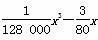 +8(0<x≤120).已知甲、乙两地相距100千米.
+8(0<x≤120).已知甲、乙两地相距100千米.
(1)当汽车以40千米/时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙 地耗油最少?最少为多少升?
地耗油最少?最少为多少升?
解析:(1)当x=40(单位:千米/时)时,汽车从甲地到乙地行驶了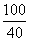 =2.5(单位:小时).要耗油
=2.5(单位:小时).要耗油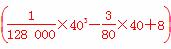 ×2.5=17.5(单位:升).所以当汽车以40千米/时的速度匀速行驶时,从甲地到乙地耗油17.5升.
×2.5=17.5(单位:升).所以当汽车以40千米/时的速度匀速行驶时,从甲地到乙地耗油17.5升.
( 2)当速度为x千米/时,汽车从甲地到乙地行驶了
2)当速度为x千米/时,汽车从甲地到乙地行驶了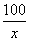 小时,设耗油量为h(x)升,依题意得h(x)=
小时,设耗油量为h(x)升,依题意得h(x)=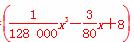 ·
·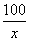 =
=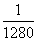 x2+
x2+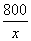 -
-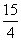 (0<x≤120).
(0<x≤120).
所以h′(x)=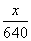 -
-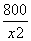 =
=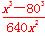 (0<x≤120).
(0<x≤120).
令h′(x)=0,得x=80.
当x∈(0,80)时,h′(x)<0,h(x)是减函数;
当x∈(80,120]时,h′(x)>0,h(x)是增函数.
所以当x=80时,h(x)取得极小值h(80)=11.25.
因此h(x)在(0,120]上只有一个极值,也是它的最小值.
所以,当汽车以80千米/时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.


科目:高中数学 来源: 题型:
做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积的价格为b元,当造价最低时,锅炉的底面直径与高的比为( )
A.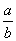 B.
B.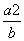 C.
C.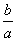 D.
D.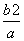
查看答案和解析>>
科目:高中数学 来源: 题型:
某工厂6年来生产某种产品的情况是:前3年年产量的增长速度越来越快,后3年年产量保持不变,则该厂6年来这种产品的总产量C与时间t(年)的函数关系图象正确的是( )
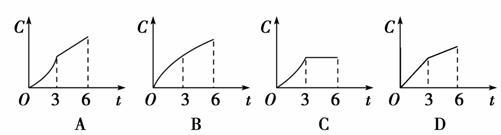
查看答案和解析>>
科目:高中数学 来源: 题型:
根据市场调查,某商品在最近40天内的价格P与时间t的关系用图1中的一条折线表示,销量Q与时间t的关系用图2中的线段表示(t∈N*).

(1)分别写出图1表示的价格与时间的函数关系P=f(t),图2表示的销售量与时间的函数关系Q=g(t);
(2)这种商品的销售额S(销售量与价格之积)的最大值及此时的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
某企业工资调整,规定如下:基本工资大于或等于600元,工资 增加20%;若小于600元大于等于400元,则工资增加15%;若小于400元,则工资增加10%.请编写一个程序,使其能根据用户输入
增加20%;若小于600元大于等于400元,则工资增加15%;若小于400元,则工资增加10%.请编写一个程序,使其能根据用户输入 的基本工资,计算出增加后的工资.
的基本工资,计算出增加后的工资.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com