（04年上海卷文）(本题满分14分) 第1小题满分6分, 第2小题满分8分
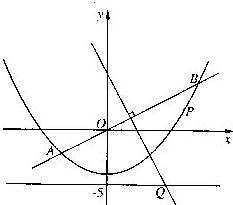
如图, 直线y=
x与抛物线y=
x2－4交于A、B两点, 线段AB的垂直平分线与直线y=－5交于Q点.
(1) 求点Q的坐标；
(2) 当P为抛物线上位于线段AB下方
(含A、B) 的动点时, 求ΔOPQ面积的最大值.
解析：(1) 解方程组 | y= | 得 | X1=－4, x2=8 |
y= | y1=－2, y2=4 |
即A(－4,－2),B(8,4), 从而AB的中点为M(2,1).
由kAB==
,直线AB的垂直平分线方程y－1=(x－2).
令y=－5, 得x=5, ∴Q(5,－5)
(2) 直线OQ的方程为x+y=0, 设P(x, 
x2－4).
∵点P到直线OQ的距离d=
=
,
,∴SΔOPQ=
=
.
∵P为抛物线上位于线段AB下方的点, 且P不在直线OQ上,
∴－4≤x<4
－4或4－4<x≤8.
∵函数y=x2+8x－32在区间[－4,8] 上单调递增,
∴当x=8时, ΔOPQ的面积取到最大值30.
阅读快车系列答案科目：高中数学 来源： 题型：
（04年上海卷文）(18分)
设P1(x1,y1), P1(x2,y2),…, Pn(xn,yn)(n≥3,n∈N) 是二次曲线C上的点, 且a1=
2, a2=
2, …, an=
2构成了一个公差为d(d≠0) 的等差数列, 其中O是坐标原点. 记Sn=a1+a2+…+an.
(1) 若C的方程为
－y2=1,n=3. 点P1(3,0) 及S3=162, 求点P3的坐标；
(只需写出一个)
(2) 若C的方程为y2=2px(p≠0). 点P1(0,0), 对于给定的自然数n, 证明：
(x1+p)2, (x2+p)2, …,(xn+p)2成等差数列；
(3) 若C的方程为
(a>b>0). 点P1(a,0), 对于给定的自然数n, 当公差d变化时, 求Sn的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
（04年上海卷文）若函数y=f(x)的图象与函数y=lg(x+1)的图象关于直线x-y=0对称,则f(x)=( )
(A)10x-1. (B) 1-10x. (C) 1-10-x. (D) 10-x-1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
时,目标函数k=3x-2y的最大值为 .