
(14分)如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.
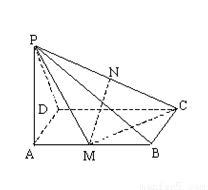
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
见解析。
【解析】
试题分析:证明:如答图所示

⑴设PD的中点为E,连结AE、NE,
由N为PD的中点知EN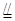
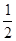 DC,
DC,
又ABCD是矩形,∴DC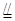 AB,∴EN
AB,∴EN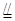
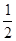 AB
AB
又M是AB的中点,∴EN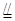 AN,
AN,
∴AMNE是平行四边形
∴MN∥AE,而AE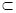 平面PAD,NM
平面PAD,NM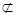 平面PAD
平面PAD
∴MN∥平面PAD
证明:⑵∵PA=AD,∴AE⊥PD,
又∵PA⊥平面ABCD,CD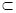 平面ABCD,
平面ABCD,
∴CD⊥PA,而CD⊥AD,∴CD⊥平面PAD
∴CD⊥AE, ∵PD∩CD=D,∴AE⊥平面PCD,
∵MN∥AE,∴MN⊥平面PCD,
又MN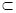 平面PMC,
平面PMC,
∴平面PMC⊥平面PCD.
考点:本题主要考查四棱锥的特征、点线面关系重大平行与垂直,考查空间想象能力及逻辑推理论证能力。
点评:证明空间问题注意转化成平面问题,充分利用平面图形的特征,这是立体几何中的基本问题。


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
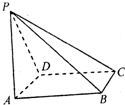 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,查看答案和解析>>
科目:高中数学 来源: 题型:
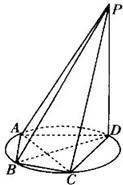 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.| 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com