
把一张纸卷到圆柱形的纸筒面上,卷上几圈.用剪刀斜着将纸筒剪断,再把卷着的纸展开,你就会看到:纸的边缘线是一条波浪形的曲线.
你知道吗?这条曲线就是正弦曲线!请你来证明这一事实.
证明:如图(1),设纸筒底面半径为1单位长,截面(椭圆面)与底面所成的二面角为θ(定值),截口的中心为O′.
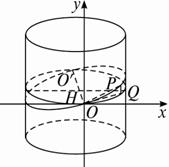
(1)
过O′作圆柱的直截面,交截口曲线于两点.取其中一点为O,在过点O且与圆柱侧面相切的平面内,以点O为坐标原点建立直角坐标系,使得Oy轴是圆柱的一条母线.
设点P是截口曲线上任意一点,点Q是点P在⊙O′所在平面内的射影,过Q作QH⊥O′O,垂足为H,连结PH,则∠PHQ是截面与底面所成二面角的平面角,所以∠PHQ=θ.又设∠QO′O=α(变量).
在图(2)中,设P点坐标为(x,y),以下分别计算P点的横坐标和纵坐标.
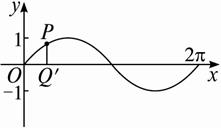
(2)
x=OQ′=![]() =α,y=Q′P=QP=QH·tanθ,
=α,y=Q′P=QP=QH·tanθ,
而在Rt△QHQ′中,QH=sinα,所以y=tanθ·sinα.
令A=tanθ(定值),则有y=Asinα.
这就证明了截口曲线是一条正弦曲线.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:训练必修四数学人教A版 人教A版 题型:044
一剪刀剪出一条正弦曲线.
把一张纸卷到圆柱形的纸筒面上,卷上几圈.用剪刀斜着将纸筒剪断,再把卷着的纸展开,你就会看到:纸的边缘线是一条波浪形的曲线.
你知道吗?这条曲线就是正弦曲线!请你来证明这一事实.
查看答案和解析>>
科目:高中数学 来源: 题型:
第一步:分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌的张数相同;
第二步:从左边一堆拿出两张,放入中间一堆;
第三步:从右边一堆拿出一张,放入中间一堆;
第四步:左边有一堆有几张牌,就从中间一堆拿出几张牌放入左边一堆.
这时,小明准确地说出了中间一堆牌现有的张数.你认为中间一堆牌的张数是____________.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四1.5函数的图象练习卷(一)(解析版) 题型:选择题
一条正弦曲线的一个最高点为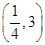 ,从相邻的最低点到这个最高点的图象交x轴于
,从相邻的最低点到这个最高点的图象交x轴于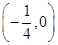 ,最低点纵坐标为-3,则此曲线的解析式为( )
,最低点纵坐标为-3,则此曲线的解析式为( )
A.y=3sin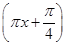
B.y=3sin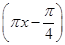
C.y=3sin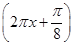
D.y=3sin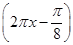
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com