
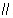 平面A1B1C1;
平面A1B1C1;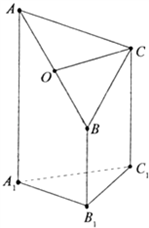
科目:高中数学 来源: 题型:
 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3查看答案和解析>>
科目:高中数学 来源: 题型:
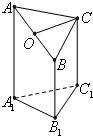
 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.查看答案和解析>>
科目:高中数学 来源:2013-2014学年黑龙江哈师大附中高三上期期中考试理科数学试卷(解析版) 题型:解答题
如图是一个直三棱柱被削去一部分后的几何体的直观图与三视图中的侧视图、俯视图.在直观图中, 是
是 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.

(1)求证:EM∥平面ABC;
(2)试问在棱DC上是否存在点N,使NM⊥平面 ? 若存在,确定
? 若存在,确定
点N的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年黑龙江哈师大附中高三上期期中考试文科数学试卷(解析版) 题型:解答题
如图是一个直三棱柱被削去一部分后的几何体的直观图与三视图中的侧视图、俯视图.在直观图中, 是
是 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.

(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求出该几何体的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com