
| 2 |
| ||
| 3 |
A、8
| ||
B、
| ||
| C、6π | ||
D、
|
| 2 |
| 2 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 2 |
| BD2+OD2 |
| ||
| 2 |
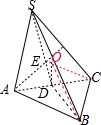
| ||
| 2 |


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
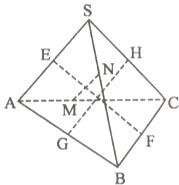 如图,在四面体S-ABC中,E、F、G、H、M、N分别是棱SA、BC、AB、SC、AC、SB的中点,且EF=GH=MN,求证:SA⊥BC,SB⊥AC,SC⊥AB.
如图,在四面体S-ABC中,E、F、G、H、M、N分别是棱SA、BC、AB、SC、AC、SB的中点,且EF=GH=MN,求证:SA⊥BC,SB⊥AC,SC⊥AB.查看答案和解析>>
科目:高中数学 来源:2010-2011学年山西省高三高考前适应性训练数学理卷 题型:选择题
在四面体S—ABC中,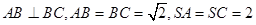 ,二面角S—AC—B的余弦值是
,二面角S—AC—B的余弦值是 ,则该四面体外接球的表面积是 ( )
,则该四面体外接球的表面积是 ( )
A.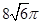 B.
B.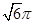 C.24
C.24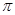 D.6
D.6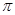
查看答案和解析>>
科目:高中数学 来源:2007-2008学年江苏省南通市启东中学高三第三次月考数学试卷(文科)(解析版) 题型:填空题
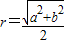 ,将此结论拓展到空间,可得出的正确结论是:在四面体S-ABC中,若SA、SB、SC两两垂直,SA=a,SB=b,SC=c,则四面体S-ABC的外接球半径R= .
,将此结论拓展到空间,可得出的正确结论是:在四面体S-ABC中,若SA、SB、SC两两垂直,SA=a,SB=b,SC=c,则四面体S-ABC的外接球半径R= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com