在1,2,3,4,5的所有排列a1,a2,a3,a4,a5中,
(1)求满足a1<a2,a2>a3,a3<a4,a4>a5的概率;
(2)记ξ为某一排列中满足ai=i(i=1,2,3,4,5)的个数,求ξ的分布列和数学期望.
分析:(1)本题是一个古典概型,试验发生包含的所有的排列种数有A55.满足条件的事件中,若a1,a3,a5取集合{1,2,3}中的元素,a2,a4取集合{4,5}中的元素,都符合要求,若a1,a3,a5取集合{1,2,4}中的元素,a2,a4取集合{3,5}中的元素,列举出结果,得到概率.
(2)ξ为某一排列中满足ai=i(i=1,2,3,4,5)的个数,由题意知ξ可以取0,1,2,3,5.结合变量对应的事件,写出变量的分布列,和期望.
解答:解:(1)由题意知,本题是一个古典概型,
试验发生包含的所有的排列种数有A
55=120个.
满足a
1<a
2,a
2>a
3,a
3<a
4,a
4>a
5的排列中,
若a
1,a
3,a
5取集合{1,2,3}中的元素,a
2,a
4取集合{4,5}中的元素,都符合要求,有A
33A
22=12个.
若a
1,a
3,a
5取集合{1,2,4}中的元素,a
2,a
4取集合{3,5}中的元素,
这时符合要求的排列只有1,3,2,5,4;2,3,1,5,4;4,5,1,3,2;4,5,2,3,1共4个.
故满足条件的概率
P==.
(2)随机变量ξ可以取0,1,2,3,5.
P(ξ=5)==,
P(ξ=3)==,
P(ξ=2)==,
P(ξ=1)==,
P(ξ=0)=1-=.
∴ξ的分布列为
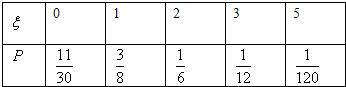
∴ξ的数学期望
Eξ=0×+1×+2×+3×+5×=1.
点评:求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,只要注意解题格式就问题不大.




 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案