
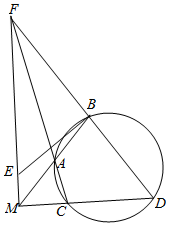
 如图,已知A,B,C,D四点共圆,BA,DC的延长线交于点M,CA,DB的延长线交于点F,连接FM,且FM⊥MD.过点B作FD的垂线,交FM于点E
如图,已知A,B,C,D四点共圆,BA,DC的延长线交于点M,CA,DB的延长线交于点F,连接FM,且FM⊥MD.过点B作FD的垂线,交FM于点E分析 (Ⅰ)利用:A,B,C,D四点共圆,可得∠FBA=∠FCD,结合公共角,即可证明△FAB∽△FDC;
(Ⅱ)证明:F,E,A,B四点共圆,利用割线定理证明MA•MB=ME•MF.
解答 证明:(Ⅰ)∵A,B,C,D四点共圆,
∴∠FBA=∠FCD,
∵∠AFB=∠DFC,
∴△FAB∽△FDC
(Ⅱ)如图,在△FBE,△FMD中,∠FBE=∠FMD=90°,∠BFE=∠MFD,
由三角形内角和定理,可得∠BEF=∠MDF,
∵ABDC为圆的内接四边形,
∴∠MDF=∠BAF,
∴∠BEF=∠BAF,
∴F,E,A,B四点共圆,
∴MA•MB=ME•MF.
点评 本题考查三角形相似的判定,考查四点共圆、圆的内接四边形的性质,考查割线定理,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | C. | A∪B=R | D. | A∩B=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
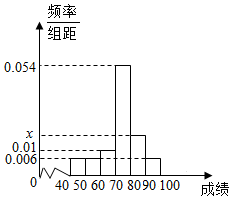 如图是某班50位学生期中考试化学成绩的频率分布直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则成绩在[70,90)内的频数为( )
如图是某班50位学生期中考试化学成绩的频率分布直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则成绩在[70,90)内的频数为( )| A. | 27 | B. | 30 | C. | 32 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
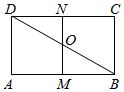 如图,矩形ABCD中AB=2,BC=$\frac{{2\sqrt{3}}}{3}$,M,N分别为AB,CD中点,BD与MN交于O,现将矩形沿MN折起,使得二面角A-MN-B的大小为$\frac{π}{3}$,则折起后cos∠DOB为( )
如图,矩形ABCD中AB=2,BC=$\frac{{2\sqrt{3}}}{3}$,M,N分别为AB,CD中点,BD与MN交于O,现将矩形沿MN折起,使得二面角A-MN-B的大小为$\frac{π}{3}$,则折起后cos∠DOB为( )| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ρ=1 | B. | ρsinθ=1 | C. | ρcosθ=1 | D. | ρ=2sinθ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | -2 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com