
����E={a1,a2,��,a100}���Ӽ�X=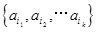 ,����X�ġ��������С�Ϊx1,x2��,x100,����
,����X�ġ��������С�Ϊx1,x2��,x100,���� =
=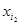 =��=
=��=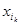 =1.�������Ϊ0,����:�Ӽ�{a2,a3}�ġ��������С�Ϊ0,1,1,0,0,��,0.
=1.�������Ϊ0,����:�Ӽ�{a2,a3}�ġ��������С�Ϊ0,1,1,0,0,��,0.
(1)�Ӽ�{a1,a3,a5}�ġ��������С���ǰ3��͵�����������;
(2)��E���Ӽ�P�ġ��������С�p1,p2,��,p100����p1=1,pi+pi+1=1,1��i��99;E���Ӽ�Q�ġ��������С�q1,q2,��,q100����q1=1,qj+qj+1+qj+2=1,1��j��98,��P��Q��Ԫ�ظ���Ϊ��������.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
���ڷǿ�ʵ���� ������
������ ����ǿ�ʵ����
����ǿ�ʵ���� ���ָ����������⣺
���ָ����������⣺
��1��������������������������ļ��� ����
����
��2��������������������������ļ���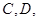 ����
���� ��
��
��3��������������������������ļ���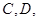 ����
���� ��
��
��4��������������������������ļ���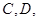 �ش��ڳ���
�ش��ڳ��� ��ʹ�ö������
��ʹ�ö������ ������
������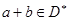 ��
��
����������ȷ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����A={x|x2-2x-3>0},B={x|x2+ax+b��0},��A��B=R,A��B={x|3<x��4},��a+b��ֵ����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�費��ʽx2��x��0�Ľ⼯ΪM������f(x)��ln(1��|x|)�Ķ�����ΪN����M��NΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�輯��A��{��1,1,3}��B��{a��2��a2��4}��A��B��{3}����ʵ��a��ֵΪ________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com