练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    当a为何实数时，曲线y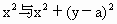＝＝1没有公共点？有一个公共点？有两个公共点？有三个公共点？有四个公共点？

    答案：
    解析：

    　　略解　由－(2a－1)y＋－1＝0，Δ＝＝－4a＋5．

    (1)当a＞时，Δ＜0，原方程组无解．

    (2)当a＝时，y＝＞0，原方程组有两解．

    (3)当a＜时，＝2a－1，－1．

    ①a∈(－1，1)时，＜0，原方程组有两解；

    ②a＝－1时，y＝0或y＝－3＜0，原方程组有一解；

    ③当a＝1时，y＝0或y＝1＞0；原方程组有三解；

    ④当1＜a＜时，＞0，＞0，原方程组有四解；

    ⑤当a＜－1时，＜0，＜0，原方程组无解．

    　　综上，当a＞或a＜－1时，两曲线无公共点；当a＝－1时，两曲线有一个公共点；当a＝或－1＜a＜1时，两曲线有两个公共点；当a＝1时，两曲线有三个公共点；当1＜a＜时，两曲线有四个公共点．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知点M（0，-1），直线l：y=mx+1与曲线C：ax2+y2=2（m，a∈R）交于A、B两点．
    （1）当m=0时，有∠AOB=
    π
    3
    ，求曲线C的方程；
    （2）当实数a为何值时，对任意m∈R，都有
    OA
    •
    OB
    为定值T？指出T的值；
    （3）设动点P满足
    MP
    =
    OA
    +
    OB
    ，当a=-2，m变化时，求点P的轨迹方程；
    （4）是否存在常数M，使得对于任意的a∈（0，1），m∈R，都有
    OA
    •
    OB
    ＜M    恒成立？如果存在，求出的M得最小值；如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点M（0，-1），直线l：y=mx+1与曲线C：ax2+y2=2（m，a∈R）交于A、B两点．
    （1）当m=0时，有∠AOB=
    π
    3
    ，求曲线C的方程；
    （2）当实数a为何值时，对任意m∈R，都有
    OA
    •
    OB
    =-2    成立．
    （3）设动点P满足
    MP
    =
    OA
    +
    OB
    ，当a=-2，m变化时，求|OP|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线l：y=mx+1与曲线C：ax2+y2=2（m、a∈R）交于A、B两点，O为坐标原点．
    （1）当m=0时，有∠AOB=
    π
    3
    ，求曲线C的方程；
    （2）当实数a为何值时，对任意m∈R，都有
    OA
    •
    OB
    为定值T？指出T的值；
    （3）已知点M（0，-1），当a=-2，m变化时，动点P满足
    MP
    =
    OA
    +
    OB
    ，求动点P的纵坐标的变化范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年周至二中四模理）( 14分)

    直线l:ax－y－1=0与曲线C：x2－2y2=1交于P、Q两点，

    (1)当实数a为何值时，|PQ|=2.

    (2)是否存在a的值，使得以PQ为直径的圆经过原点？若存在，求出a的值；若不存在，说明理由.

    查看答案和解析>>

    同步练习册答案