
对于下列命题:①函数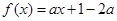 在区间
在区间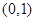 内有零点的充分不必要条件是
内有零点的充分不必要条件是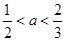 ;②已知
;②已知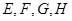 是空间四点,命题甲:
是空间四点,命题甲: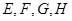 四点不共面,命题乙:直线
四点不共面,命题乙:直线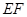 和
和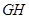 不相交,则甲是乙成立的充分不必要条件;③“
不相交,则甲是乙成立的充分不必要条件;③“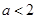 ”是“对任意的实数
”是“对任意的实数 ,
,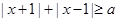 恒成立”的充要条件;④“
恒成立”的充要条件;④“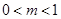 ”是“方程
”是“方程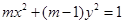 表示双曲线”的充分必要条件.其中所有真命题的序号是 .
表示双曲线”的充分必要条件.其中所有真命题的序号是 .
科目:高中数学 来源: 题型:填空题
给出以下四个命题,所有真命题的序号为________.
①从总体中抽取样本(x1,y1),(x2,y2),…,(xn,yn),若记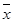 =
=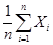 ,
,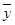 =
= i,则回归直线
i,则回归直线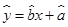 必过点(
必过点(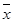 ,
,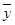 );
);
②将函数y=cos 2x的图象向右平移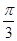 个单位,得到函数y=sin
个单位,得到函数y=sin 的图象;
的图象;
③已知数列{an},那么“对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上”是“{an}为等差数列”的充分不必要条件;
④命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|≥2,则-2<x<2”.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
有下列命题:①空间四点共面,则其中必有三点共线;②空间四点不共面,则其中任何三点不共线;③空间四点中有三点共线,则此四点共面;④空间四点中任何三点不共线,则此四点不共面.其中正确的命题是________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com