
 ,对于下列三个命题:①f(x)是偶函数;②f(x)<1;③当x=
,对于下列三个命题:①f(x)是偶函数;②f(x)<1;③当x= 时,f(x)取得极小值.其中真命题的序号为
时,f(x)取得极小值.其中真命题的序号为 的性质,只须考虑当0<x<
的性质,只须考虑当0<x< 时的函数值即可,再利用单位圆中的三角函数线,通过面积关系证明sinx<x.对于③,利用商的导数运算法则及基本初等函数的导数公式,求出函数的导数,然后根据导函数的符号确定函数的单调性即可得到结论.
时的函数值即可,再利用单位圆中的三角函数线,通过面积关系证明sinx<x.对于③,利用商的导数运算法则及基本初等函数的导数公式,求出函数的导数,然后根据导函数的符号确定函数的单调性即可得到结论. 的定义域为x≠0,
的定义域为x≠0,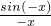 =
=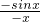 =
= =f(x),
=f(x), 的性质,只须考虑当0<x<
的性质,只须考虑当0<x< 时的函数值即可,
时的函数值即可,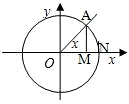 如图,在单位圆中,有sinx=MA,
如图,在单位圆中,有sinx=MA,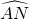 的长为l,则x=
的长为l,则x=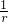 =l,
=l, ON•MA<
ON•MA< ON•x,即MA<x,
ON•x,即MA<x, <1,
<1,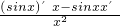 =
=
 =0得xcosx-sinx=0,
=0得xcosx-sinx=0, π时,不满足tanx=x,
π时,不满足tanx=x, π时,f(x)取不到极小值,故③错.
π时,f(x)取不到极小值,故③错.

科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com