
分析 此题要求f(3)的值,须知f(x)的解析式,即求出p,q的值;已知条件是|f(x)|≤2对于1≤x≤5恒成立,所以问题转化为f(x)在区间[1,5]的值域问题,即f(x)在[1,5]的值域为[-2,2]恒成立,因为元函数含有待定系数所以单调性不确定,故需讨论对称轴的位置以确定f(x)的单调性,从而确定其值域,进而确定p,q的取值.具体讨论过程分为3步:对称轴在1的左边则递增;在5的右边则递减;在1和5之间时,单调性不唯一,所以还需分情况讨论,讨论何时取得的最大值.
解答 解:函数${f}_{(x)}={x}^{2}-px+q$对于?x∈[1,5]有不等式|f(x)|≤2恒成立,
∴函数在[1,5]上的值域为[-2,2]恒成立,
函数f(x)的对称轴为$x=-\frac{b}{2a}=-\frac{-p}{2×1}=\frac{p}{2}$,故分类讨论如下:
1).当$x=\frac{p}{2}<1,即p<2$时,函数在[1,5]上为单调增函数,
∴其值域为[f(1),f(5)],满足条件$\left\{\begin{array}{l}{{f}_{(1)}={1}^{2}-1p+q≥-2}\\{{f}_{(5)}={5}^{2}-5p+q≤2}\end{array}\right.$即可,求得p≥5,与p<2矛盾,故不合题意舍去;
2).当$x=\frac{p}{2}>5,即p>10$时,函数在[1,5]上为单调减函数,
∴其值域为[f(5),f(1)],满足条件$\left\{\begin{array}{l}{{f}_{(5)}={5}^{2}-5p+q≥-2}\\{{f}_{(1)}={1}^{2}-1p+q≤2}\end{array}\right.$即可,求得p≤7,与p>10矛盾,故不合题意舍去;
3).当$1≤x=\frac{p}{2}≤5,即2≤p≤10$时,函数在[1,5]上单调性不唯一,所以需要根据对称轴的位置再分类;
a).当$1≤x=\frac{p}{2}<3,即2≤p<6$时,函数在[1,5]上先为减函数后为增函数,并在x=5时取得最大值,在$x=\frac{p}{2}$时取得最小值,
∴其值域为$[{f}_{(\frac{p}{2})},{f}_{(5)}]$,满足条件$\left\{\begin{array}{l}{{f}_{(\frac{p}{2})}=(\frac{p}{2})^{2}-p×\frac{p}{2}+q≥-2}\\{{f}_{(5)}={5}^{2}-5p+q≤2}\end{array}\right.$即可,求得6≤p≤14,与2≤p<6矛盾,故不合题意舍去;
b).当$3<x=\frac{p}{2}≤5,即6<p≤10$时,函数在[1,5]上先为减函数后为增函数,并在x=1时取得最大值,在$x=\frac{p}{2}$时取得最小值,
∴其值域为$[{f}_{(\frac{p}{2})},{f}_{(1)}]$,满足条件$\left\{\begin{array}{l}{{f}_{(\frac{p}{2})}=(\frac{p}{2})^{2}-p×(\frac{p}{2})+q≥-2}\\{{f}_{(1)}={1}^{2}-1p+q≤2}\end{array}\right.$即可,求得-2≤p≤6,与6<p≤10矛盾,故不合题意舍去;
c).当$x=\frac{p}{2}=3,即p=6$时,函数在[1,5]上关于x=3对称,最大值为f(1)=f(5),最小值为f(3),
∴其值域为[f(3),f(1)],此时韩式解析式为${f}_{(x)}={x}^{2}-6x+q$,满足条件$\left\{\begin{array}{l}{{f}_{(3)}={3}^{2}-6×3+q≥-2}\\{{f}_{(1)}={1}^{2}-6×1+q≤2}\end{array}\right.$,求得$\left\{\begin{array}{l}{q≥7}\\{q≤7}\end{array}\right.$
∴q=7,函数解析式为${f}_{(x)}={x}^{2}-6x+7$,所以f(3)=-2
故:答案应填-2
点评 本题虽是关于二次函数的不等式恒成立问题,但是本质上是考察对二次函数的值域掌握情况,运用分类讨论的方法确定二次函数的单调性,进而确定函数的值域,从而确定待定系数的值求出解析式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
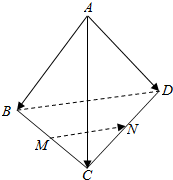 已知空间四边形ABCD,连接AC、BD,设M,N分别是BC,CD的中点,则$\overrightarrow{MN}$用$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$表示的结果为$\frac{1}{2}\overrightarrow{AD}$$-\frac{1}{2}\overrightarrow{AB}$.
已知空间四边形ABCD,连接AC、BD,设M,N分别是BC,CD的中点,则$\overrightarrow{MN}$用$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$表示的结果为$\frac{1}{2}\overrightarrow{AD}$$-\frac{1}{2}\overrightarrow{AB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{21}$ | B. | $\frac{4}{21}$ | C. | $\frac{5}{21}$ | D. | $\frac{11}{42}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | 2-$\sqrt{3}$ | C. | $\sqrt{5}$-2 | D. | $\sqrt{6}$-$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com