
| A�� | 24��Ԫ | B�� | 27��Ԫ | C�� | 30��Ԫ | D�� | 33��Ԫ |
���� ��ÿ��������x������y��������z��Ԫ������Լ��������Ŀ�꺯�����������Թ滮��֪ʶ������⣮
��� �⣺��ÿ��������x������y��������z��Ԫ��
��Լ������Ϊ$\left\{\begin{array}{l}{3x+y��13}\\{2x+3y��18}\\{x+2y��8}\\{x��y��N}\end{array}\right.$��Ŀ�꺯��z=5x+3y��
��������ʽ���Ӧ��ƽ��������ͼ��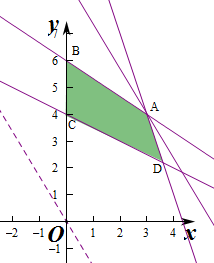
��z=5x+3y��y=-$\frac{5}{3}x+\frac{z}{3}$��
ƽ��ֱ��y=-$\frac{5}{3}x+\frac{z}{3}$������ͼ���֪��ֱ��y=-$\frac{5}{3}x+\frac{z}{3}$������Aʱֱ��y=-$\frac{5}{3}x+\frac{z}{3}$�Ľؾ����
��ʱz���
��$\left\{\begin{array}{l}{3x+y=13}\\{2x+3y=18}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$����A��3��4����
��ʱz=5��3+3��4=15+12=27����Ԫ����
���ó�ÿ��ɻ�õ��������Ϊ27����Ԫ����
��ѡ��B
���� ������Ҫ�������Թ滮��Ӧ�����⣬�����������Լ�������Լ�Ŀ�꺯�����������ν���ǽ������Ĺؼ���


 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
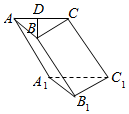 ��ͼ����������ABC-A1B1C1�У���A1B1C1=90�㣬A1B1=B1C1=AA1=2����C�ڵ���A1B1C1�ϵ���ӰA1C1�ߵ��е㣬DΪAC���е㣬��E��CC1�ϣ���$\overrightarrow{{C}_{1}E}$=��$\overrightarrow{{C}_{1}C}$��0���ˣ�1��
��ͼ����������ABC-A1B1C1�У���A1B1C1=90�㣬A1B1=B1C1=AA1=2����C�ڵ���A1B1C1�ϵ���ӰA1C1�ߵ��е㣬DΪAC���е㣬��E��CC1�ϣ���$\overrightarrow{{C}_{1}E}$=��$\overrightarrow{{C}_{1}C}$��0���ˣ�1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �������� | B�� | �������� | C�� | ������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3��6�� | B�� | ��-10��8�� | C�� | ��3��2�� | D�� | ��7��6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����֪AB��ԲO��ֱ������C��D�ǰ�Բ�����������ȷֵ㣬$\overrightarrow{AB}$=$\overrightarrow{a}$��$\overrightarrow{AD}$=$\overrightarrow{b}$����$\overrightarrow{AC}$=��������
��ͼ��ʾ����֪AB��ԲO��ֱ������C��D�ǰ�Բ�����������ȷֵ㣬$\overrightarrow{AB}$=$\overrightarrow{a}$��$\overrightarrow{AD}$=$\overrightarrow{b}$����$\overrightarrow{AC}$=��������| A�� | $\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B�� | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | C�� | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D�� | -$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\overrightarrow{a}$•$\overrightarrow{b}$��•$\overrightarrow{c}$=$\overrightarrow{a}$•��$\overrightarrow{b}$•$\overrightarrow{c}$�� | B�� | $\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$����$\overrightarrow{b}$=$\overrightarrow{c}$ | ||
| C�� | |$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | D�� | ��|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|����$\overrightarrow{a}$•$\overrightarrow{b}$=0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com