
 );如果它是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为3,按照上述变换规则,我们得到一个数列:3,10,5,16,8,4,2,1.对科拉茨(Lothar Collatz)猜想,目前谁也不能证明,更不能否定.现在请你研究:如果对正整数n(首项)按照上述规则施行变换(注:1可以多次出现)后的第六项为1,则n的所有可能的取值为________.
);如果它是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为3,按照上述变换规则,我们得到一个数列:3,10,5,16,8,4,2,1.对科拉茨(Lothar Collatz)猜想,目前谁也不能证明,更不能否定.现在请你研究:如果对正整数n(首项)按照上述规则施行变换(注:1可以多次出现)后的第六项为1,则n的所有可能的取值为________. );如果它是奇数,则将它乘3加1(即3n+1),我们可以从第六项为1出发,逆向逐项即可求出n的所有可能的取值.
);如果它是奇数,则将它乘3加1(即3n+1),我们可以从第六项为1出发,逆向逐项即可求出n的所有可能的取值. );如果它是奇数,则将它乘3加1(即3n+1),是解答本题的关键.
);如果它是奇数,则将它乘3加1(即3n+1),是解答本题的关键. 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
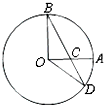 (几何证明选讲选做题)如图4,A,B是圆O上的两点,且OA⊥OB,OA=2,C为OA的中点,连接BC并延长交圆O于点D,则CD=________.
(几何证明选讲选做题)如图4,A,B是圆O上的两点,且OA⊥OB,OA=2,C为OA的中点,连接BC并延长交圆O于点D,则CD=________.查看答案和解析>>
科目:高中数学 来源: 题型:单选题



查看答案和解析>>
科目:高中数学 来源: 题型:解答题
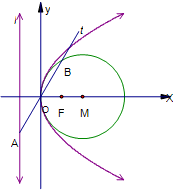 如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为 的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.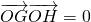 ,求△GOH面积的最小值;
,求△GOH面积的最小值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
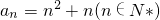 ,试判断{△an},{△2an}是否为等差或等比数列,并说明理由;
,试判断{△an},{△2an}是否为等差或等比数列,并说明理由;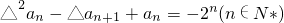 ,求数列{an}的通项公式.
,求数列{an}的通项公式.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com