
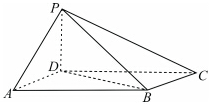
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.分析 (Ⅰ)因为∠DAB=60°,AB=2AD,由余弦定理得BD=$\sqrt{3}$AD,利用勾股定理证明BD⊥AD,根据PD⊥底面ABCD,易证BD⊥PD,根据线面垂直的判定定理和性质定理,可证PA⊥BD;
(II)要求棱锥D-PBC的高.只需证BC⊥平面PBD,然后得平面PBC⊥平面PBD,作DE⊥PB于E,则DE⊥平面PBC,利用勾股定理可求得DE的长.
解答 (Ⅰ)证明:因为∠DAB=60°,AB=2AD,
由余弦定理得$BD=\sqrt{3}AD$.…(1分)
从而BD2+AD2=AB2,∴BD⊥AD,…(3分)
又由PD⊥底面ABCD,BD?面ABCD,可得BD⊥PD.…(4分)
所以BD⊥平面PAD.故PA⊥BD.…(6分)
(Ⅱ)解:作DE⊥PB,垂足为E.
已知PD⊥底面ABCD,则PD⊥BC,
由(Ⅰ)知BD⊥AD,又BC∥AD,所以BC⊥BD.
故BC⊥平面PBD,BC⊥DE.
则DE⊥平面PBC.…(8分)
由题设知,PD=2,则$BD=2\sqrt{3}$,PB=4,…(10分)
根据DE•PB=PD•BD,得$DE=\sqrt{3}$,
即点D到面PBC的距离为$\sqrt{3}$.…(12分)
点评 此题是个中档题.考查线面垂直的性质定理和判定定理,以及点到面的距离,查了同学们观察、推理以及创造性地分析问题、解决问题能力.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,+∞) | B. | (-5,-$\frac{3}{2}$) | C. | (-$\frac{3}{2}$,1) | D. | (-$\frac{3}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{3\sqrt{5}}}{2}$ | B. | $-\frac{{3\sqrt{15}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{3\sqrt{10}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-3} | B. | {x|x≥-3} | C. | {x|x<-3} | D. | {x|x≤-3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com