
【题目】在平面直角坐标系xOy中,已知圆M:(x+1)2+y2= ![]() 的圆心为M,圆N:(x﹣1)2+y2=
的圆心为M,圆N:(x﹣1)2+y2= ![]() 的圆心为N,一动圆与圆M内切,与圆N外切.
的圆心为N,一动圆与圆M内切,与圆N外切.
(Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)过点(1,0)的直线l与曲线P交于A,B两点,若 ![]() =﹣2,求直线l的方程.
=﹣2,求直线l的方程.
【答案】解:(Ⅰ)设动圆P的半径为r,则|PM|= ![]() ﹣r,|PN|=r+
﹣r,|PN|=r+ ![]() .
.
两式相加,得|PM|+PN|=4>|MN|,
由椭圆定义知,点P的轨迹是以M、N为焦点,焦距为2,实轴长为4的椭圆,其方程为 ![]() .
.
(Ⅱ)当直线的斜率不存在时,直线l的方程为x=1,则 ![]() ,
, ![]() ,
, ![]() .当直线的斜率存在时,设直线l的方程为y=k(x﹣1),设A(x1,y1),B(x2,y2),联立
.当直线的斜率存在时,设直线l的方程为y=k(x﹣1),设A(x1,y1),B(x2,y2),联立 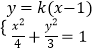 消去y,得(3+4k2)x2﹣8k2x+4k2﹣12=0,则有
消去y,得(3+4k2)x2﹣8k2x+4k2﹣12=0,则有 ![]() ,
, ![]() ,
, ![]() =
= ![]() =
= ![]() .
.
由已知,得 ![]() ,解得
,解得 ![]() .
.
故直线l的方程为 ![]()
【解析】(Ⅰ)根据两圆内外切的性质可得出|PM|+PN|=4>|MN|,即为椭圆由已知可求出方程。(Ⅱ)分情况讨论直线斜率存在和不存在,当斜率不存在时不成立;而当斜率存在时,设出直线方程和椭圆联立,消去y 由韦达定理求出 x 1 + x 2、 x1x2 的值,代入到向量的数量积坐标运算公式即可求出 k的值进而得出直线方程。
【考点精析】认真审题,首先需要了解椭圆的概念(平面内与两个定点![]() ,
,![]() 的距离之和等于常数(大于
的距离之和等于常数(大于![]() )的点的轨迹称为椭圆,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距).
)的点的轨迹称为椭圆,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距).


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+2ax﹣a﹣1,x∈[0,2],a为常数.
(1)用g(x)表示f(x)的最小值,求g(a)的解析式;
(2)在(1)中,是否存在最小的整数m,使得g(a)﹣m≤0对于任意a∈R均成立,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)如果对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得函数
,使得函数![]() 的最大值为0,若存在,求出
的最大值为0,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市郊区有一加油站,2018年初汽油的存储量为50吨,计划从年初起每周初均购进汽油![]() 吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前
吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前![]() 个周需求量
个周需求量![]() 吨与
吨与![]() 的函数关系式为
的函数关系式为![]()
![]() ,
, ![]() 为常数,且前4个周城区内汽车的汽油需求量为100吨.
为常数,且前4个周城区内汽车的汽油需求量为100吨.
(1)试写出第![]() 个周结束时,汽油存储量
个周结束时,汽油存储量![]() (吨)与
(吨)与![]() 的函数关系式;
的函数关系式;
(2)要使16个周内每周按计划购进汽油之后,加油站总能满足城区内和城外的需求,且每周结束时加油站的汽油存储量不超过150吨,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)函数![]() 若存在
若存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数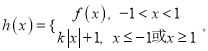 讨论函数
讨论函数![]() 的零点个数(直接写出答案,不要求写出解题过程).
的零点个数(直接写出答案,不要求写出解题过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=AA1=4,AB=3,AB⊥AC.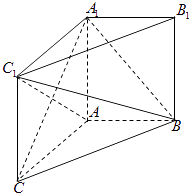
(Ⅰ)求证:A1C⊥平面ABC1;
(Ⅱ)求二面角A﹣BC1﹣A1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且 ![]() =λ(0<λ<1).
=λ(0<λ<1).
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利民中学为了了解该校高一年级学生的数学成绩,从高一年级期中考试成绩中抽出100名学生的成绩,由成绩得到如下的频率分布直方图.
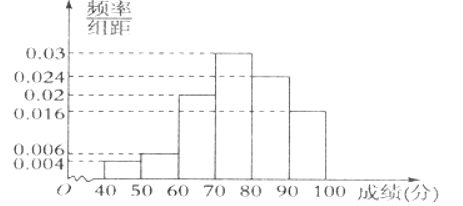
根据以上频率分布直方图,回答下列问题:
(1)求这100名学生成绩的及格率;(大于等于60分为及格)
(2)试比较这100名学生的平均成绩和中位数的大小.(精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com