
等差数列{an}中,a1=-8,它的前16项的平均值是7,若从中抽取一项,余下的15项的平均值为7.2,则抽取的是( )
A.第7项 B.第8项
C.第15项 D.第16项
科目:高中数学 来源: 题型:
若集合A={x|-1≤2x+1≤3}, B=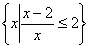 ,则A∩B=( )
,则A∩B=( )
A.{x|-1≤x<0} B.{x|0<x≤1}
C.{x|0≤x≤2} D.{x|0≤x≤1}
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,货轮在海上以50海里/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155o的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为125o.半小时后,货轮到达C点处,观测到灯塔A的方位角为80o.求此时货轮与灯塔之间的距离(得数保留最简根号).

查看答案和解析>>
科目:高中数学 来源: 题型:
关于x的方程x2-xcosA·cosB-cos2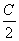 =0有一个根为1,则此三角形为( )
=0有一个根为1,则此三角形为( )
A.等腰三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
已知正项数列{an}的前n项和为Sn,且an和Sn满足:4Sn=(an+1)2(n=1,2,3……),
(1)求{an}的通项公式;
(2)设bn= ,求{bn}的前n项和Tn;
,求{bn}的前n项和Tn;
(3)在(2)的条件下,对任意n∈N*,Tn> 都成立,求整数m的最大值.
都成立,求整数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某良种培育基地正在培育一种小麦新品种A,将其与原有的一个优良品种B进行对照
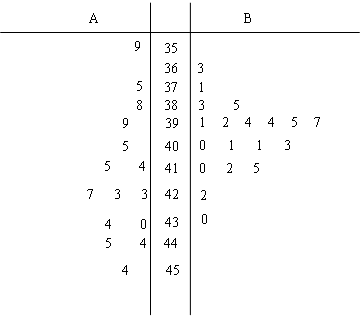
试验,两种小麦共种植了34亩,所得亩产数据(单位:千克)如下
(I)用茎叶图处理现有的数据,有什么优点?
(II)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论。
 xkb1.com
xkb1.com
w w w .x k b 1.c o m
查看答案和解析>>
科目:高中数学 来源: 题型:
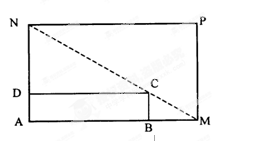
如图所示,将一矩形花坛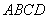 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园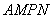 ,要求
,要求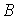 在
在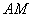 上,
上,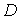 在
在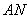 上,且对角线
上,且对角线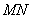 过
过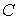 点,已知
点,已知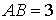 米,
米,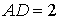 米.
米.
 ⑴要使矩形
⑴要使矩形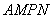 的面积大于32平方米,则
的面积大于32平方米,则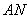 的长应
的长应 在什么范围内?
在什么范围内?
 ⑵当
⑵当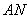 的长度是多少时,矩形
的长度是多少时,矩形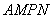 的面积最小?并求最小面积;
的面积最小?并求最小面积;
⑶若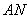 的长度不少于6米,则当
的长度不少于6米,则当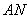 的长度是多少时,矩形
的长度是多少时,矩形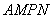 的面积最小?
的面积最小?
并求出最小 面积.
面积.




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com