
已知正项数列{an}的前n项和为Sn,且an和Sn满足:4Sn=(an+1)2(n=1,2,3……),
(1)求{an}的通项公式;
(2)设bn= ,求{bn}的前n项和Tn;
,求{bn}的前n项和Tn;
(3)在(2)的条件下,对任意n∈N*,Tn> 都成立,求整数m的最大值.
都成立,求整数m的最大值.
∵4Sn=(an+1)2, ①
∴4Sn-1=(an-1+1)2(n≥2), ②
①-②得
4(Sn-Sn-1)=(an+1)2-(an-1+1)2.
∴4an=(an+1)2-(an-1+1)2.
化简得(an+an-1)·(an-an-1-2)=0.
∵an>0,∴an-an-1=2(n≥2).
∴{an}是以1为首项,2为公差的等差数列.
∴an=1+(n-1)·2=2n-1.
(2)bn= =
=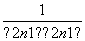 =
=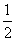 (
(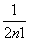 -
-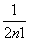 ).
).
∴Tn=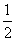
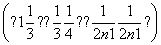
=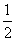 (1-
(1-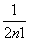 )=
)=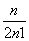
(3)由(2)知Tn=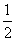 (1-
(1-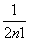 ),
),
Tn+1-Tn=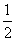 (1-
(1-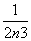 )-
)-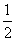 (1-
(1-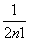 )
)
=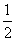 (
(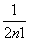 -
-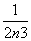 )>0.
)>0.
∴数列{Tn}是递增数列.
∴[Tn]min=T1=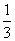 .
.
∴ <
<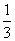 ,∴m<
,∴m<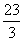 .
.
∴整数m的最大值是7.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:
等差数列{an}中,a1=-8,它的前16项的平均值是7,若从中抽取一项,余下的15项的平均值为7.2,则抽取的是( )
A.第7项 B.第8项
C.第15项 D.第16项
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com