
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,-1),离心率e=$\frac{\sqrt{6}}{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,-1),离心率e=$\frac{\sqrt{6}}{3}$.分析 (1)由题意结合隐含条件解关于a,b,c的方程组,求得a,b的值,则椭圆方程可求;
(2)设P(x1,y1),Q(x2,y2),通过斜率计算可得${{x}_{1}}^{2}+{{x}_{2}}^{2}=12$,分x1=x2、x1≠x2两种情况讨论,利用点到直线的距离公式、三角形面积公式计算即得结论.
解答 解:(1)由题意得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{6}}{3}}\\{\frac{9}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得:a2=12,b2=4.
∴椭圆C的方程为$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{4}=1$;
(2)结论:四边形PQP1Q1的面积为定值.
理由如下:
由题意得:四条垂线的方程为:x=±2$\sqrt{3}$,y=±2,
则A(2$\sqrt{3}$,2),B(-2$\sqrt{3}$,2),
∴${k}_{OA}•{k}_{OB}=-\frac{1}{3}$.
设P(x1,y1),Q(x2,y2),则$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}=-\frac{1}{3}$(*)
PQ=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$.
∵点P、Q在椭圆C上,∴${{y}_{1}}^{2}=4(1-\frac{{{x}_{1}}^{2}}{12}),{{y}_{2}}^{2}=4(1-\frac{{{x}_{2}}^{2}}{12})$,
将(*)式平方得:${{x}_{1}}^{2}{{x}_{2}}^{2}=9×16(1-\frac{{{x}_{1}}^{2}}{12})(1-\frac{{{x}_{2}}^{2}}{12})$,即${{x}_{1}}^{2}+{{x}_{2}}^{2}=12$,
①若x1=x2,则P、P1、Q、Q1分别是直线OA、OB与椭圆的交点,
∴四个点的坐标为:($\sqrt{6},\sqrt{2}$),($-\sqrt{6},-\sqrt{2}$),(-$\sqrt{6},\sqrt{2}$),($\sqrt{6},-\sqrt{2}$),
∴四边形PQP1Q1的面积为$8\sqrt{3}$;
②若x1≠x2,则直线PQ的方程可设为:$y-{y}_{1}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}(x-{x}_{1})$,
化简得:(y2-y1)x-(x2-x1)y+x2y1-x1y2=0,
∴点O到直线PQ的距离为d=$\frac{|{x}_{1}{y}_{2}-{x}_{2}{y}_{1}|}{\sqrt{({x}_{2}-{x}_{1})^{2}+({y}_{2}-{y}_{1})^{2}}}$,
∴△OPQ的面积S=$\frac{1}{2}$PQ•d=$\frac{1}{2}$|x1y2-x2y1|=$\frac{1}{2}$$\sqrt{{{x}_{1}}^{2}{{y}_{2}}^{2}-2{x}_{1}{x}_{2}{y}_{1}{y}_{2}+{{x}_{2}}^{2}{{y}_{1}}^{2}}$
=$\frac{1}{2}$$\sqrt{4({{x}_{1}}^{2}+{{x}_{2}}^{2})}$=$\frac{1}{2}\sqrt{4×12}=2\sqrt{3}$.
根据椭圆的对称性,故四边形PQP1Q1的面积为4S,即为定值$8\sqrt{3}$.
综上:四边形PQP1Q1的面积为定值$8\sqrt{3}$.
点评 本题是一道直线与圆锥曲线的综合题,考查椭圆的标准方程、点的坐标、点到直线的距离、三角形面积公式,韦达定理等基础知识,考查分类讨论的思想,考查运算求解能力,注意解题方法的积累,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
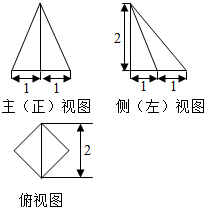 已知某棱锥的三视图如图所示,俯视图为正方形,根据图中所给的数据.那么该棱锥的表面积是( )
已知某棱锥的三视图如图所示,俯视图为正方形,根据图中所给的数据.那么该棱锥的表面积是( )| A. | 8+4$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | 2$\sqrt{2}$+2$\sqrt{3}$ | D. | 2+2$\sqrt{2}$+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com