解:(1)∵f(x)=
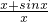
,∴f'(x)=

设g(x)=xcosx-sinx,x∈(0,π).则g'(x)=-xsinx<0
∴g(x)在(0,π)上为减函数
又∵g(0)=0,∴当x∈(0,π)时,g(x)<0,
∴当x∈(0,π)时,f'(x)=

<0,可得f(x)在区间(0,π)上是减函数 …(5分)
(2)显然,当a=0、1时,或x=0、π时,不等式成立
当0<a<1且0<x<π时,原不等式等价于:(1-a)sin(1-a)x≥(1-2a)sinx.
下面证明一个更强的不等式:(1-a)sin(1-a)x≥(1-2a+a
2)sinx.…①
即sin(1-a)x≥(1-a)sinx.…②
亦即

≥

由(1)知

在(0,π)上为减函数
又∵(1-a)x≤x,∴

≥

,得不等式②成立,从而①成立
∵(1-2a+a
2)sinx≥(1-2a)sinx.
∴(1-a)sin(1-a)x≥(1-2a)sinx.
综上所述,得0≤x≤π,且0≤a≤1时,原不等式成立 …(12分)
分析:(1)对函数f(x)求导数,得f'(x)=

,再讨论分子对应函数的单调性,得f'(x)的分子最大值小于0,从而得到f'(x)<0在区间(0,π)上恒成立,所以f(x)是区间(0,π)上的减函数;
(2)为了证明原不等式,利用(1)中的单调性,证明出不等式(1-a)sin(1-a)x≥(1-2a+a
2)sinx区间(0,π)上恒成立.结合(1-2a+a
2)sinx≥(1-2a)sinx得(1-a)sin(1-a)x≥(1-2a)sinx,移项整理即得原不等式成立.
点评:本题给出含三角函数的分式函数,求函数的单调性并证明不等式恒成立,着重考查了利用导数研究函数的单调性和不等式恒成立等知识,属于中档题.

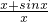 .
.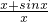 ,∴f'(x)=
,∴f'(x)=
 <0,可得f(x)在区间(0,π)上是减函数 …(5分)
<0,可得f(x)在区间(0,π)上是减函数 …(5分) ≥
≥
 在(0,π)上为减函数
在(0,π)上为减函数  ≥
≥ ,得不等式②成立,从而①成立
,得不等式②成立,从而①成立 ,再讨论分子对应函数的单调性,得f'(x)的分子最大值小于0,从而得到f'(x)<0在区间(0,π)上恒成立,所以f(x)是区间(0,π)上的减函数;
,再讨论分子对应函数的单调性,得f'(x)的分子最大值小于0,从而得到f'(x)<0在区间(0,π)上恒成立,所以f(x)是区间(0,π)上的减函数;

 备战中考寒假系列答案
备战中考寒假系列答案