练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （本小题满分12分）某工厂用万元钱购买了一台新机器，运输安装费用千元，每年投保、动力消耗的费用也为千元，每年的保养、维修、更换易损零件的费用逐年增加，第一年为千元，第二年为千元，第三年为千元，依此类推，即每年增加千元．
    （Ⅰ）求使用年后，保养、维修、更换易损零件的累计费用S（千元）关于的表达式；
    （Ⅱ）问这台机器最佳使用年限是多少年？并求出年平均费用（单位：千元）的最小值．(最佳使用年限是指使年平均费用最小的时间，年平均费用=（购入机器费用+运输安装费用+每年投保、动力消耗的费用+保养、维修、更换易损零件的累计费用）÷机器使用的年数 )
    （Ⅰ）（Ⅱ）最佳年限是12年，平均费用为15．５千元

    试题分析：(Ⅰ)由题易知其费用成等差数列，                                   ……2分
    所以                                         ……5分
    (Ⅱ)设使用年的年平均费用为，则  
                                               ……10分
    当且仅当时，取等号，取最小值 ，                                   ……11分
    故最佳年限是12年，平均费用为15．５千元.                                  ……12分
    点评：根据实际问题抽象出函数的解析式后，只需利用基本不等式就可求得函数的最值，但是一定要注意在定义域（使实际问题有意义的自变量的取值范围）内求解.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    已知是定义在上的奇函数，当时的图像如图，那么不等式的解集是
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    当时，函数和的图象只可能是  （  ）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (本小题15分)已知函数.
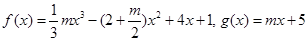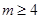    (1)当时,求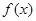的单调递增区间;
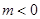    (2)是否存在,使得对任意的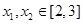,都有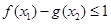恒成立.若存在,求出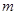的取值范围; 若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数的图象是（   ）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若直角坐标平面内M、N两点满足：
    ①点M、N都在函数f(x)的图像上；
    ②点M、N关于原点对称，则称这两点M、N是函数f(x)的一对“靓点”。
    已知函数则函数f(x)有          对“靓点”。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某公司为了实现1000万元利润的目标，准备制定一个激励销售人员的奖励方案：在销售利润达到10万元时，按销售利润进行奖励，且奖金（单位：万元）随销售利润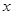（单位：万元）的增加而增加，但奖金总数不超过5万元，同时奖金不能超过利润的％.现有三个奖励模型：，分析与推导哪个函数模型能符合该公司的要求？并给予证明．（注：）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数的图象是（   ）


     
     

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若函数y=f(x)的图象与函数g(x)=()x-1的图象关于原点对称，则f(2)=______.

    查看答案和解析>>

    同步练习册答案