
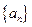 满足
满足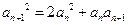 , 且
, 且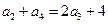 ,
,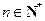 .
.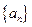 的通项公式;
的通项公式; 数列
数列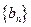 的前
的前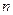 项和为
项和为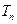 ,令
,令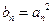 ,其中
,其中 ,试比较
,试比较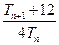 与
与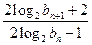 的大小,并加以证明.
的大小,并加以证明.
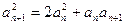 ,即
,即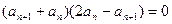
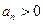 ,所以有
,所以有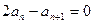 ,所以
,所以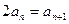
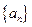 是公比为
是公比为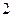 的等比数列. …………………………………………3分
的等比数列. …………………………………………3分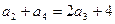 得
得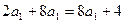 , 解得
, 解得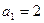 .
.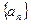 的通项公式为
的通项公式为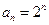
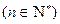 . ……………………………………….6分
. ……………………………………….6分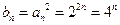 ,所以
,所以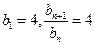
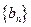 是首项为
是首项为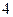 ,公比是
,公比是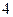 的等比数列.
的等比数列. 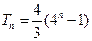 ,……………………………………….……………………………………7分
,……………………………………….……………………………………7分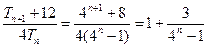
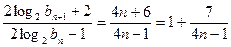 . ……………………………………8分
. ……………………………………8分
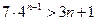
 时,
时,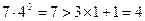 ,上面不等式显然成立;
,上面不等式显然成立;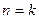 时,不等式
时,不等式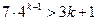 成立
成立 时,
时,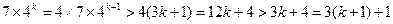 .
. 均有
均有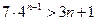 ……………………………………….10分
……………………………………….10分 ,
,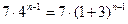
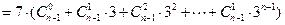
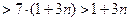 .
. 均有
均有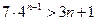 . ……………………………………..10分
. ……………………………………..10分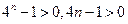 ,
, 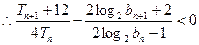
 均有
均有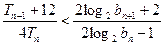 . …………………
. ………………… ……….12分
……….12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com