
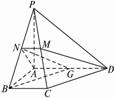
(1)求证:PB⊥DM;
(2)求CD与平面ADMN所成的角.
解法一:(1)证明:∵N是PB的中点,PA=AB,?
∴AN⊥PB.?
∵AD⊥平面PAB,∴AD⊥PB.?
从而PB⊥平面ADMN.?
∵DM ![]() 面ADMN,
面ADMN,
∴PB⊥DM.?
(2)如图,取AD的中点C,连结BG,NG,
则BG∥CD,?

∴BG与平面ADMN所成的角和CD与平面ADMN所成的角相等.?
∵PB⊥平面ADMN,?
∴∠BGN是BG与平面ADMN所成的角.?
在Rt△BGH中,
sin∠BGN=![]() =
=![]() .?
.?
故CD与平面ADMN所成的角是arcsin![]() .
.
解法二:如图,以A为坐标原点建立空间直角坐标系A—xyz,设BC=1,则A(0,0,0)?,P(0,0,2),B(2,0,0),C(2,1,0),M(1,![]() ,1),D(0,2,0).?
,1),D(0,2,0).?
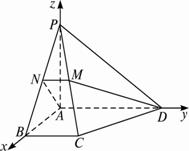
(1)∵![]() ·
·![]() =(2,0,-2)·(1,-
=(2,0,-2)·(1,-![]() ,1)=0,?
,1)=0,?
∴PB⊥DM.?
(2)∵![]() ·
·![]() =(2,0,-2)·(0,2,0)=0,?
=(2,0,-2)·(0,2,0)=0,?
∴PB⊥AD,又因为PB⊥DM,?
∴PB⊥平面ADMN.
∵〈![]() ,
,![]() 〉的余角即是CD与平面ADMN所成的角.?
〉的余角即是CD与平面ADMN所成的角.?
∵cos〈![]() ,
,![]() 〉=
〉=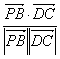 =
=![]() .?
.?
∴CD与平面ADMN所成的角为arcsin![]() .?
.?
点评:本题主要考查空间线线、线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:高中数学 来源: 题型:
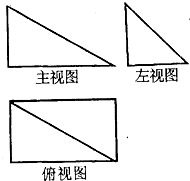 已知四棱锥P-ABCD的三视图如右图.该棱锥中,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在棱BC上移动.
已知四棱锥P-ABCD的三视图如右图.该棱锥中,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在棱BC上移动.查看答案和解析>>
科目:高中数学 来源:新课标高三数学空间图形的基本关系与公理、空间图形的平行关系专项训练(河北) 题型:解答题
如右图所示,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,点F是PB的中点,点E在边BC上移动.
 (1)求三棱锥E—PAD的体积;
(1)求三棱锥E—PAD的体积;
(2)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在边BC的何处,都有PE⊥AF.
查看答案和解析>>
科目:高中数学 来源:新课标高三数学空间图形的平行关系、垂直关系专项训练(河北) 题型:解答题
如右图所示,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,点F是PB的中点,点E在边BC上移动.
(1)求三棱锥E—PAD的体积;
(2)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在边BC的何处,都有PE⊥AF.
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求证:BE⊥PD;
(2)求异面直线AE与CD所成角的大小.(用反三角函数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com