
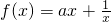 且a>0
且a>0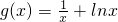 ,若f(x)与g(x)的图象在区间(1,e2)上有两个不同的交点,求实数a的取值范围.
,若f(x)与g(x)的图象在区间(1,e2)上有两个不同的交点,求实数a的取值范围. (2分)
(2分)
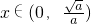 时,f′(x)<0,即f(x)在
时,f′(x)<0,即f(x)在 上单调递减
上单调递减 时,f′(x)>0,即f(x)在
时,f′(x)>0,即f(x)在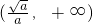 上单调递增 (4分)
上单调递增 (4分)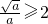 ,即
,即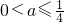 时,
时,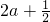
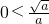 <2,即a>
<2,即a> 时,
时, 递减,在
递减,在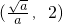 递增,故
递增,故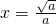 时 f(x)min=
时 f(x)min=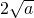 .
.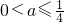 时,f(x)min=
时,f(x)min=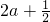 ;a>
;a> 时,f(x)min=
时,f(x)min=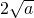 .
.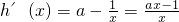
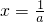
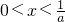 ,所以h(x)的减区间
,所以h(x)的减区间 ;
; ,所以h(x)的增区间
,所以h(x)的增区间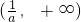 .
.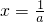 ,h(x)取极小值
,h(x)取极小值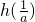 且
且 .
.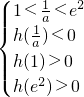 ,解得
,解得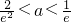
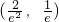 .(12分)
.(12分)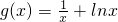 ,f(x)与g(x)的图象在区间(1,e2)上有两个不同的交点,即h(x)=f(x)-g(x)=ax-lnx(x>0)有两个零点,故可利用导数研究出函数的单调性,找出函数h(x)有两个零点的条件,由此条件解出实数a的取值范围;
,f(x)与g(x)的图象在区间(1,e2)上有两个不同的交点,即h(x)=f(x)-g(x)=ax-lnx(x>0)有两个零点,故可利用导数研究出函数的单调性,找出函数h(x)有两个零点的条件,由此条件解出实数a的取值范围;

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
已知函数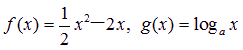 (a>0,且a≠1),其中为常数.如果
(a>0,且a≠1),其中为常数.如果![]() 是增函数,且
是增函数,且![]() 存在零点(
存在零点(![]() 为
为![]() 的导函数).
的导函数).
(Ⅰ)求a的值;
(Ⅱ)设A(x1,y1)、B(x2,y2)(x1<x2)是函数y=g(x)的图象上两点,![]() (
(![]() 为
为![]() 的导函数),证明:
的导函数),证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源:2007-2008学年重庆市西南师大附中高一(上)期末数学试卷(解析版) 题型:解答题
 (a>0且a≠1).
(a>0且a≠1).查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省名校新高考研究联盟高三(下)5月联考数学试卷(文科)(解析版) 题型:选择题
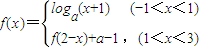 (a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( )
(a>0且a≠1),若x1≠x2,且f(x1)=f(x2),则x1+x2的值( )查看答案和解析>>
科目:高中数学 来源:2009-2010学年北京市朝阳区高二(下)期末数学试卷(理科)(解析版) 题型:解答题
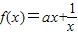 且a>0
且a>0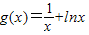 ,若f(x)与g(x)的图象在区间(1,e2)上有两个不同的交点,求实数a的取值范围.
,若f(x)与g(x)的图象在区间(1,e2)上有两个不同的交点,求实数a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com